Refine listing
Actions for selected content:
220 results in 46Exx
ENTROPY AND RENORMALIZED SOLUTIONS FOR THE p(x)-LAPLACIAN EQUATION WITH MEASURE DATA
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 82 / Issue 3 / December 2010
- Published online by Cambridge University Press:
- 18 August 2010, pp. 459-479
- Print publication:
- December 2010
-
- Article
-
- You have access
- Export citation
Orthogonally additive holomorphic functions of bounded type over C(K)
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 53 / Issue 3 / October 2010
- Published online by Cambridge University Press:
- 12 August 2010, pp. 609-618
-
- Article
-
- You have access
- Export citation
Transitivity in spaces of vector-valued functions
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 53 / Issue 3 / October 2010
- Published online by Cambridge University Press:
- 05 August 2010, pp. 601-608
-
- Article
-
- You have access
- Export citation
WEAK-STAR PROPERTIES OF HOMOMORPHISMS FROM WEIGHTED CONVOLUTION ALGEBRAS ON THE HALF-LINE
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 89 / Issue 1 / August 2010
- Published online by Cambridge University Press:
- 20 July 2010, pp. 75-90
- Print publication:
- August 2010
-
- Article
-
- You have access
- Export citation
FAMILIES OF FRACTIONAL FANTAPPIÈ TRANSFORMS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 82 / Issue 1 / August 2010
- Published online by Cambridge University Press:
- 07 April 2010, pp. 62-78
- Print publication:
- August 2010
-
- Article
-
- You have access
- Export citation
DERIVATIVE-FREE CHARACTERIZATIONS OF COMPACT GENERALIZED COMPOSITION OPERATORS BETWEEN ZYGMUND TYPE SPACES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 81 / Issue 3 / June 2010
- Published online by Cambridge University Press:
- 17 March 2010, pp. 398-408
- Print publication:
- June 2010
-
- Article
-
- You have access
- Export citation
SHARP CONSTANTS BETWEEN EQUIVALENT NORMS IN WEIGHTED LORENTZ SPACES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 88 / Issue 1 / February 2010
- Published online by Cambridge University Press:
- 22 January 2010, pp. 19-27
- Print publication:
- February 2010
-
- Article
-
- You have access
- Export citation
THE FATOU COMPLETION OF A FRÉCHET FUNCTION SPACE AND APPLICATIONS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 88 / Issue 1 / February 2010
- Published online by Cambridge University Press:
- 08 December 2009, pp. 49-60
- Print publication:
- February 2010
-
- Article
-
- You have access
- Export citation
INVERSE IMAGES OF SECTORS BY FUNCTIONS IN WEIGHTED BERGMAN–ORLICZ SPACES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 86 / Issue 2 / April 2009
- Published online by Cambridge University Press:
- 01 April 2009, pp. 233-247
- Print publication:
- April 2009
-
- Article
-
- You have access
- Export citation
Composition operators on μ-Bloch spaces
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 61 / Issue 1 / 01 February 2009
- Published online by Cambridge University Press:
- 20 November 2018, pp. 50-75
- Print publication:
- 01 February 2009
-
- Article
-
- You have access
- Export citation
Weighted composition operators on Orlicz-Sobolev spaces
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 83 / Issue 3 / December 2007
- Published online by Cambridge University Press:
- 09 April 2009, pp. 327-334
- Print publication:
- December 2007
-
- Article
-
- You have access
- Export citation
Extrapolation of the functional calculus of generalized Dirac operators and related embedding and Littlewood-Paley-type theorems. I
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 83 / Issue 3 / December 2007
- Published online by Cambridge University Press:
- 09 April 2009, pp. 297-326
- Print publication:
- December 2007
-
- Article
-
- You have access
- Export citation
Multidimensional Hausdorff operators on the real Hardy space
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 83 / Issue 1 / August 2007
- Published online by Cambridge University Press:
- 09 April 2009, pp. 79-86
- Print publication:
- August 2007
-
- Article
-
- You have access
- Export citation
A note on the boundedness of Bergman-type operators on mixed norm spaces
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 82 / Issue 3 / June 2007
- Published online by Cambridge University Press:
- 09 April 2009, pp. 395-402
- Print publication:
- June 2007
-
- Article
-
- You have access
- Export citation
Derivative-free characterizations of Qk spaces
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 82 / Issue 2 / April 2007
- Published online by Cambridge University Press:
- 09 April 2009, pp. 283-295
- Print publication:
- April 2007
-
- Article
-
- You have access
- Export citation
Spaces of vector functions that are integrable with respect to vector measures
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 82 / Issue 1 / February 2007
- Published online by Cambridge University Press:
- 09 April 2009, pp. 85-109
- Print publication:
- February 2007
-
- Article
-
- You have access
- Export citation
Semicontinuous functions and convex sets in C(K) spaces
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 82 / Issue 1 / February 2007
- Published online by Cambridge University Press:
- 09 April 2009, pp. 111-121
- Print publication:
- February 2007
-
- Article
-
- You have access
- Export citation
Growth properties and sequences of zeros of analytic functions in spaces of Dirichlet type
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 80 / Issue 3 / June 2006
- Published online by Cambridge University Press:
- 09 April 2009, pp. 397-418
- Print publication:
- June 2006
-
- Article
-
- You have access
- Export citation
Some new Besov and Triebel-Lizorkin spaces associated with para-accretive functions on spaces of homogeneous type
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 80 / Issue 2 / April 2006
- Published online by Cambridge University Press:
- 09 April 2009, pp. 229-262
- Print publication:
- April 2006
-
- Article
-
- You have access
- Export citation
Topologies on spaces of vector-valued meromorphic functions
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 78 / Issue 2 / April 2005
- Published online by Cambridge University Press:
- 09 April 2009, pp. 273-290
- Print publication:
- April 2005
-
- Article
-
- You have access
- Export citation
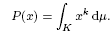
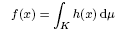
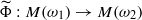 to a homomorphism between the corresponding weighted measure algebras on ℝ
to a homomorphism between the corresponding weighted measure algebras on ℝ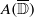 every nonzero homomorphism
every nonzero homomorphism 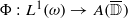 extends uniquely to a continuous homomorphism
extends uniquely to a continuous homomorphism 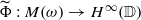 which is also continuous with respect to the weak-star topologies. Similarly, for a large class of Beurling algebras
which is also continuous with respect to the weak-star topologies. Similarly, for a large class of Beurling algebras 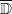 (including the algebra of absolutely convergent Taylor series on
(including the algebra of absolutely convergent Taylor series on 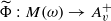 which is also continuous with respect to the weak-star topologies.
which is also continuous with respect to the weak-star topologies.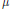
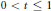
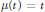
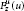
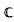 ” with an application to Gleason's problem.
” with an application to Gleason's problem.