Refine listing
Actions for selected content:
161 results in 30Cxx
Sharp starlikeness conditions for analytic functions with bounded derivative
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 69 / Issue 3 / December 2000
- Published online by Cambridge University Press:
- 09 April 2009, pp. 303-315
- Print publication:
- December 2000
-
- Article
-
- You have access
- Export citation
On Symmetric Quasicircles
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 68 / Issue 1 / February 2000
- Published online by Cambridge University Press:
- 09 April 2009, pp. 131-144
- Print publication:
- February 2000
-
- Article
-
- You have access
- Export citation
Functions with unbounded ∂-derivative and their boundary functions
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 63 / Issue 1 / August 1997
- Published online by Cambridge University Press:
- 09 April 2009, pp. 100-109
- Print publication:
- August 1997
-
- Article
-
- You have access
- Export citation
On convex and starlike functions in a sector
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 60 / Issue 3 / June 1996
- Published online by Cambridge University Press:
- 09 April 2009, pp. 363-368
- Print publication:
- June 1996
-
- Article
-
- You have access
- Export citation
Coefficients of an analytic function subordination class determined by rotations
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 60 / Issue 2 / April 1996
- Published online by Cambridge University Press:
- 09 April 2009, pp. 245-254
- Print publication:
- April 1996
-
- Article
-
- You have access
- Export citation
On the logarithmic coefficients of close-to-convex functions
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 60 / Issue 1 / February 1996
- Published online by Cambridge University Press:
- 09 April 2009, pp. 1-6
- Print publication:
- February 1996
-
- Article
-
- You have access
- Export citation
Matrix transformations of series of orthogonal polynomials
- Part of
-
- Journal:
- Mathematika / Volume 42 / Issue 2 / December 1995
- Published online by Cambridge University Press:
- 26 February 2010, pp. 427-443
- Print publication:
- December 1995
-
- Article
- Export citation
Hyperbolic linear invariance and hyperbolic k-convexity
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 58 / Issue 1 / February 1995
- Published online by Cambridge University Press:
- 09 April 2009, pp. 73-93
- Print publication:
- February 1995
-
- Article
-
- You have access
- Export citation
Two sharp inequalities for the norm of a factor of a polynomial
- Part of
-
- Journal:
- Mathematika / Volume 39 / Issue 2 / December 1992
- Published online by Cambridge University Press:
- 26 February 2010, pp. 341-349
- Print publication:
- December 1992
-
- Article
- Export citation
Euclidean linear invariance and uniform local convexity
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 52 / Issue 3 / June 1992
- Published online by Cambridge University Press:
- 09 April 2009, pp. 401-418
- Print publication:
- June 1992
-
- Article
-
- You have access
- Export citation
Star-center points of univalent functions
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 51 / Issue 1 / August 1991
- Published online by Cambridge University Press:
- 09 April 2009, pp. 95-105
- Print publication:
- August 1991
-
- Article
-
- You have access
- Export citation
Function classes related to Ruscheweyh derivatives
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 47 / Issue 3 / December 1989
- Published online by Cambridge University Press:
- 09 April 2009, pp. 438-444
- Print publication:
- December 1989
-
- Article
-
- You have access
- Export citation
On discontinuity of l2-angle
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 47 / Issue 2 / October 1989
- Published online by Cambridge University Press:
- 09 April 2009, pp. 269-279
- Print publication:
- October 1989
-
- Article
-
- You have access
- Export citation
Positive Harmonic Functions and Complete Metrics
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 32 / Issue 3 / 01 September 1989
- Published online by Cambridge University Press:
- 20 November 2018, pp. 286-297
- Print publication:
- 01 September 1989
-
- Article
-
- You have access
- Export citation
A gap condition for the zeroes of certain polynomials in Kaplan classes K(α, β)
- Part of
-
- Journal:
- Mathematika / Volume 34 / Issue 1 / June 1987
- Published online by Cambridge University Press:
- 26 February 2010, pp. 53-63
- Print publication:
- June 1987
-
- Article
- Export citation
Extremal problems for a class of functions of positive real part and applications
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 41 / Issue 2 / October 1986
- Published online by Cambridge University Press:
- 09 April 2009, pp. 152-164
- Print publication:
- October 1986
-
- Article
-
- You have access
- Export citation
A variational method for the construction of convergent iterative sequences
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 41 / Issue 1 / August 1986
- Published online by Cambridge University Press:
- 09 April 2009, pp. 51-58
- Print publication:
- August 1986
-
- Article
-
- You have access
- Export citation
Jakubowski starlike integral operators
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 37 / Issue 1 / August 1984
- Published online by Cambridge University Press:
- 09 April 2009, pp. 117-127
- Print publication:
- August 1984
-
- Article
-
- You have access
- Export citation
The transformation of concentric circles into concentric rectangles
- Part of
-
- Journal:
- Mathematika / Volume 28 / Issue 1 / June 1981
- Published online by Cambridge University Press:
- 26 February 2010, pp. 141-152
- Print publication:
- June 1981
-
- Article
- Export citation
An integral mean inequality for starlike functions
- Part of
-
- Journal:
- Mathematika / Volume 28 / Issue 1 / June 1981
- Published online by Cambridge University Press:
- 26 February 2010, pp. 88-98
- Print publication:
- June 1981
-
- Article
- Export citation
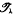 }, where
}, where 
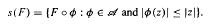
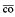
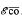
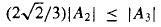 for
for 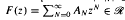 . We also prove that if
. We also prove that if 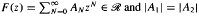 , then
, then 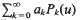 given by
given by 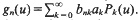 . We establish necessary and sufficient conditions on the matrix (
. We establish necessary and sufficient conditions on the matrix (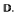 The concept of linear invariance has proved fruitful in geometric function theory. One aspect of Pommerenke's work is the extension of certain results from classical univalent function theory to linearly invariant functions. We propose a definition of a related concept that we call hyperbolic linear invariance for locally schlicht holomorphic functions that map the unit disk into itself. We obtain results for hyperbolic linearly invariant functions which generalize parts of the theory of bounded univalent functions. There are many similarities between linearly invariant functions and hyperbolic linearly invariant functions, but some new phenomena also arise in the study of hyperbolic linearly invariant functions.
The concept of linear invariance has proved fruitful in geometric function theory. One aspect of Pommerenke's work is the extension of certain results from classical univalent function theory to linearly invariant functions. We propose a definition of a related concept that we call hyperbolic linear invariance for locally schlicht holomorphic functions that map the unit disk into itself. We obtain results for hyperbolic linearly invariant functions which generalize parts of the theory of bounded univalent functions. There are many similarities between linearly invariant functions and hyperbolic linearly invariant functions, but some new phenomena also arise in the study of hyperbolic linearly invariant functions.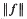 be the maximum of
be the maximum of 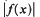 on the unit circle. We prove that
on the unit circle. We prove that 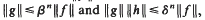 , where β =
, where β =  be the class of normalized univalent functions in the unit disk. For
be the class of normalized univalent functions in the unit disk. For  where
where  is the interior of
is the interior of 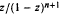 is starlike of order α 0 ≤ α < 1. We determine extreme points, inclusion relations, and show how this family acts under various linear operators.
is starlike of order α 0 ≤ α < 1. We determine extreme points, inclusion relations, and show how this family acts under various linear operators.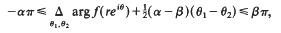
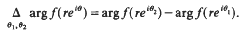
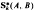 and the radius of convexity for
and the radius of convexity for 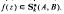 .
.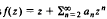 regular and satisfying │
regular and satisfying │