Refine listing
Actions for selected content:
161 results in 30Cxx
EXTREME POINTS OF INTEGRAL FAMILIES OF ANALYTIC FUNCTIONS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 94 / Issue 2 / April 2013
- Published online by Cambridge University Press:
- 14 March 2013, pp. 202-221
- Print publication:
- April 2013
-
- Article
-
- You have access
- Export citation
HOLOMORPHIC FUNCTIONS WITH IMAGE OF GIVEN LOGARITHMIC OR ELLIPTIC CAPACITY
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 94 / Issue 2 / April 2013
- Published online by Cambridge University Press:
- 08 March 2013, pp. 145-157
- Print publication:
- April 2013
-
- Article
-
- You have access
- Export citation
LIPSCHITZ SPACES AND BOUNDED MEAN OSCILLATION OF HARMONIC MAPPINGS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 88 / Issue 1 / August 2013
- Published online by Cambridge University Press:
- 18 January 2013, pp. 143-157
- Print publication:
- August 2013
-
- Article
-
- You have access
- Export citation
UNIVALENCE CRITERIA AND ANALOGUES OF THE JOHN CONSTANT
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 88 / Issue 3 / December 2013
- Published online by Cambridge University Press:
- 12 December 2012, pp. 423-434
- Print publication:
- December 2013
-
- Article
-
- You have access
- Export citation
CONFORMAL SLIT MAPS IN APPLIED MATHEMATICS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 53 / Issue 3 / January 2012
- Published online by Cambridge University Press:
- 17 September 2012, pp. 171-189
-
- Article
-
- You have access
- Export citation
Location of geodesics and isoperimetric inequalities in Denjoy domains
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 55 / Issue 1 / February 2012
- Published online by Cambridge University Press:
- 15 June 2011, pp. 245-269
-
- Article
-
- You have access
- Export citation
LANDAU’S THEOREM AND MARDEN CONSTANT FOR HARMONIC ν-BLOCH MAPPINGS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 84 / Issue 1 / August 2011
- Published online by Cambridge University Press:
- 10 June 2011, pp. 19-32
- Print publication:
- August 2011
-
- Article
-
- You have access
- Export citation
ON HARMONIC BLOCH SPACES IN THE UNIT BALL OF ℂn
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 84 / Issue 1 / August 2011
- Published online by Cambridge University Press:
- 10 June 2011, pp. 67-78
- Print publication:
- August 2011
-
- Article
-
- You have access
- Export citation
DIFFERENTIAL SUBORDINATIONS FOR CLASSES OF MEROMORPHIC p-VALENT FUNCTIONS DEFINED BY MULTIPLIER TRANSFORMATIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 83 / Issue 3 / June 2011
- Published online by Cambridge University Press:
- 05 April 2011, pp. 353-368
- Print publication:
- June 2011
-
- Article
-
- You have access
- Export citation
NEIGHBOURHOODS OF UNIVALENT FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 83 / Issue 2 / April 2011
- Published online by Cambridge University Press:
- 14 September 2010, pp. 210-219
- Print publication:
- April 2011
-
- Article
-
- You have access
- Export citation
SMALE’S PROBLEM FOR CRITICAL POINTS ON CERTAIN TWO RAYS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 88 / Issue 2 / April 2010
- Published online by Cambridge University Press:
- 25 March 2010, pp. 183-191
- Print publication:
- April 2010
-
- Article
-
- You have access
- Export citation
UNIVALENT HARMONIC MAPPINGS INTO TWO-SLIT DOMAINS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 88 / Issue 1 / February 2010
- Published online by Cambridge University Press:
- 22 January 2010, pp. 61-73
- Print publication:
- February 2010
-
- Article
-
- You have access
- Export citation
INVERSE IMAGES OF SECTORS BY FUNCTIONS IN WEIGHTED BERGMAN–ORLICZ SPACES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 86 / Issue 2 / April 2009
- Published online by Cambridge University Press:
- 01 April 2009, pp. 233-247
- Print publication:
- April 2009
-
- Article
-
- You have access
- Export citation
ON INFINITESIMAL TEICHMÜLLER SPACE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 78 / Issue 2 / October 2008
- Published online by Cambridge University Press:
- 01 October 2008, pp. 293-300
- Print publication:
- October 2008
-
- Article
-
- You have access
- Export citation
The zeros of random polynomials cluster uniformly near the unit circle
- Part of
-
- Journal:
- Compositio Mathematica / Volume 144 / Issue 3 / May 2008
- Published online by Cambridge University Press:
- 01 May 2008, pp. 734-746
- Print publication:
- May 2008
-
- Article
-
- You have access
- Export citation
Quasiregular self-mappings of manifolds and word hyperbolic groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 143 / Issue 6 / November 2007
- Published online by Cambridge University Press:
- 01 November 2007, pp. 1613-1622
- Print publication:
- November 2007
-
- Article
-
- You have access
- Export citation
Smale's mean value conjecture for odd polynomials
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 75 / Issue 3 / December 2003
- Published online by Cambridge University Press:
- 09 April 2009, pp. 409-412
- Print publication:
- December 2003
-
- Article
-
- You have access
- Export citation
Unbounded analytic functions on plane domains
- Part of
-
- Journal:
- Mathematika / Volume 50 / Issue 1-2 / December 2003
- Published online by Cambridge University Press:
- 26 February 2010, pp. 207-214
- Print publication:
- December 2003
-
- Article
- Export citation
Extremal partitions and distortion under the Montel bounded univalent maps
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 73 / Issue 3 / December 2002
- Published online by Cambridge University Press:
- 09 April 2009, pp. 419-432
- Print publication:
- December 2002
-
- Article
-
- You have access
- Export citation
The zeros of linear combinations of translates of polynomials
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 72 / Issue 1 / February 2002
- Published online by Cambridge University Press:
- 09 April 2009, pp. 109-118
- Print publication:
- February 2002
-
- Article
-
- You have access
- Export citation
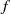
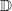
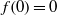
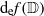
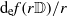
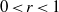
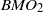
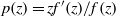
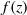
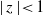
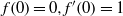
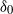
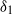
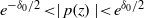
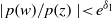
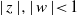
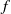
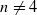 ), then every quasiregular mapping
), then every quasiregular mapping 