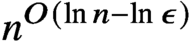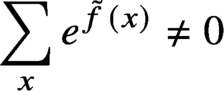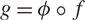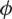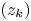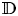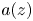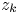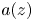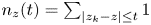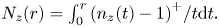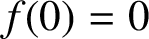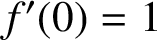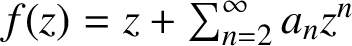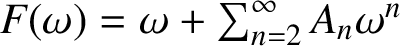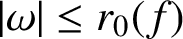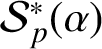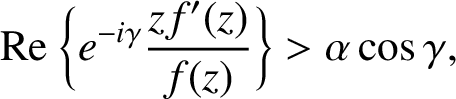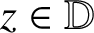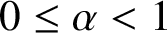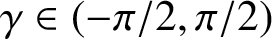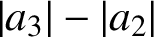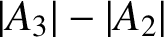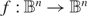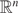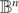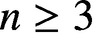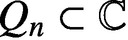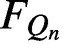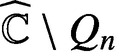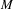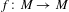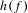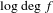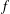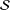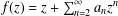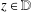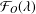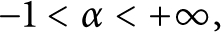Refine listing
Actions for selected content:
161 results in 30Cxx
Julia sets of Zorich maps
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 2 / February 2023
- Published online by Cambridge University Press:
- 15 November 2021, pp. 692-728
- Print publication:
- February 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
SECOND HANKEL DETERMINANT OF LOGARITHMIC COEFFICIENTS OF CONVEX AND STARLIKE FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 3 / June 2022
- Published online by Cambridge University Press:
- 30 September 2021, pp. 458-467
- Print publication:
- June 2022
-
- Article
- Export citation
A REVIEW OF ONE-PHASE HELE-SHAW FLOWS AND A LEVEL-SET METHOD FOR NONSTANDARD CONFIGURATIONS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 63 / Issue 3 / July 2021
- Published online by Cambridge University Press:
- 23 September 2021, pp. 269-307
-
- Article
- Export citation
More on zeros and approximation of the Ising partition function
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 07 June 2021, e46
-
- Article
-
- You have access
- Open access
- Export citation
Permutable quasiregular maps
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 173 / Issue 1 / July 2022
- Published online by Cambridge University Press:
- 03 June 2021, pp. 105-121
- Print publication:
- July 2022
-
- Article
-
- You have access
- Open access
- Export citation
Une note sur la densité des zéros des sommes partielles de la fonction zeta de Dedekind sur un corps quadratique
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 24 May 2021, pp. 409-415
- Print publication:
- June 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Geometric series expansion of the Neumann–Poincaré operator: Application to composite materials
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 33 / Issue 3 / June 2022
- Published online by Cambridge University Press:
- 11 May 2021, pp. 560-585
-
- Article
- Export citation
Peaking and interpolation by complex polynomials
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 64 / Issue 2 / May 2021
- Published online by Cambridge University Press:
- 05 May 2021, pp. 129-138
-
- Article
- Export citation
On non-separated zero sequences of solutions of a linear differential equation
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 64 / Issue 2 / May 2021
- Published online by Cambridge University Press:
- 30 April 2021, pp. 247-261
-
- Article
- Export citation
A NOTE ON SPIRALLIKE FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 25 March 2021, pp. 117-123
- Print publication:
- February 2022
-
- Article
- Export citation
Bohr phenomenon for operator-valued functions
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 64 / Issue 1 / February 2021
- Published online by Cambridge University Press:
- 08 January 2021, pp. 72-86
-
- Article
- Export citation
Quasiconformality and hyperbolic skew
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 171 / Issue 3 / November 2021
- Published online by Cambridge University Press:
- 18 December 2020, pp. 449-466
- Print publication:
- November 2021
-
- Article
- Export citation
CORRIGENDUM TO THE PAPER D. KALAJ, ON KELLOGG’S THEOREM FOR QUASICONFORMAL MAPPINGS. GLASG. MATH. J. 54, NO. 3, 599–603 (2012)
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 64 / Issue 1 / January 2022
- Published online by Cambridge University Press:
- 18 December 2020, p. 252
- Print publication:
- January 2022
-
- Article
-
- You have access
- Export citation
Bohr theorems for slice regular functions over octonions
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 5 / October 2021
- Published online by Cambridge University Press:
- 21 October 2020, pp. 1595-1610
- Print publication:
- October 2021
-
- Article
- Export citation
STARLIKENESS AND CONVEXITY OF CAUCHY TRANSFORMS ON REGULAR POLYGONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 103 / Issue 2 / April 2021
- Published online by Cambridge University Press:
- 05 October 2020, pp. 291-302
- Print publication:
- April 2021
-
- Article
- Export citation
INTEGRAL MEANS OF UNIVALENT FUNCTIONS ON AN ANNULUS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 103 / Issue 3 / June 2021
- Published online by Cambridge University Press:
- 21 September 2020, p. 512
- Print publication:
- June 2021
-
- Article
-
- You have access
- Export citation
Continuity of condenser capacity under holomorphic motions
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 2 / June 2021
- Published online by Cambridge University Press:
- 29 June 2020, pp. 340-348
- Print publication:
- June 2021
-
- Article
- Export citation
Entropy in uniformly quasiregular dynamics
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 8 / August 2021
- Published online by Cambridge University Press:
- 22 June 2020, pp. 2397-2427
- Print publication:
- August 2021
-
- Article
- Export citation
ON THE DIFFERENCE OF COEFFICIENTS OF OZAKI CLOSE-TO-CONVEX FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 103 / Issue 1 / February 2021
- Published online by Cambridge University Press:
- 18 June 2020, pp. 124-131
- Print publication:
- February 2021
-
- Article
- Export citation
Hyperbolic metric and membership of conformal maps in the Bergman space
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 1 / March 2021
- Published online by Cambridge University Press:
- 06 May 2020, pp. 174-181
- Print publication:
- March 2021
-
- Article
- Export citation