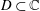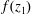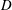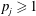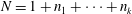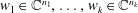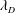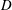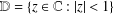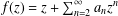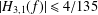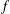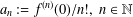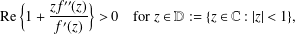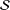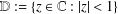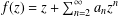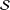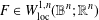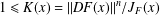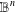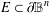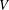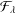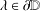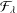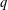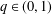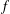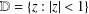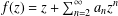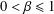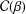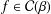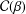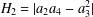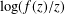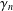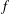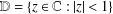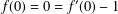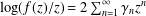Refine listing
Actions for selected content:
161 results in 30Cxx
Extension Operators for Biholomorphic Mappings
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 62 / Issue 3 / September 2019
- Published online by Cambridge University Press:
- 07 January 2019, pp. 671-679
- Print publication:
- September 2019
-
- Article
-
- You have access
- Export citation
LARGE-SCALE SUBLINEARLY LIPSCHITZ GEOMETRY OF HYPERBOLIC SPACES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 6 / November 2020
- Published online by Cambridge University Press:
- 19 December 2018, pp. 1831-1876
- Print publication:
- November 2020
-
- Article
- Export citation
ON OZAKI CLOSE-TO-CONVEX FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 99 / Issue 1 / February 2019
- Published online by Cambridge University Press:
- 20 September 2018, pp. 89-100
- Print publication:
- February 2019
-
- Article
-
- You have access
- Export citation
On a Criterion of Local Invertibility and Conformality for Slice Regular Quaternionic Functions
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 62 / Issue 1 / February 2019
- Published online by Cambridge University Press:
- 28 August 2018, pp. 97-105
-
- Article
- Export citation
CONTINUITY OF ROOTS, REVISITED
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 98 / Issue 3 / December 2018
- Published online by Cambridge University Press:
- 15 August 2018, pp. 448-455
- Print publication:
- December 2018
-
- Article
-
- You have access
- Export citation
On the existence of harmonic mappings between doubly connected domains
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 148 / Issue 3 / June 2018
- Published online by Cambridge University Press:
- 22 April 2018, pp. 619-628
- Print publication:
- June 2018
-
- Article
- Export citation
THE SHARP BOUND FOR THE HANKEL DETERMINANT OF THE THIRD KIND FOR CONVEX FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 97 / Issue 3 / June 2018
- Published online by Cambridge University Press:
- 04 April 2018, pp. 435-445
- Print publication:
- June 2018
-
- Article
-
- You have access
- Export citation
TOEPLITZ DETERMINANTS WHOSE ELEMENTS ARE THE COEFFICIENTS OF ANALYTIC AND UNIVALENT FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 97 / Issue 2 / April 2018
- Published online by Cambridge University Press:
- 26 February 2018, pp. 253-264
- Print publication:
- April 2018
-
- Article
-
- You have access
- Export citation
UNIQUENESS THEOREMS FOR MAPPINGS OF FINITE DISTORTION
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 104 / Issue 3 / June 2018
- Published online by Cambridge University Press:
- 07 November 2017, pp. 412-429
- Print publication:
- June 2018
-
- Article
-
- You have access
- Export citation
Applications of differential subordinations for norm estimates of an integral operator
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 148 / Issue 2 / April 2018
- Published online by Cambridge University Press:
- 06 November 2017, pp. 281-291
- Print publication:
- April 2018
-
- Article
- Export citation
MAPPING PROPERTIES OF A SCALE INVARIANT CASSINIAN METRIC AND A GROMOV HYPERBOLIC METRIC
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 97 / Issue 1 / February 2018
- Published online by Cambridge University Press:
- 18 August 2017, pp. 141-152
- Print publication:
- February 2018
-
- Article
-
- You have access
- Export citation
A SCHWARZ LEMMA FOR
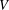 $V$ -HARMONIC MAPS AND THEIR APPLICATIONS
$V$ -HARMONIC MAPS AND THEIR APPLICATIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 96 / Issue 3 / December 2017
- Published online by Cambridge University Press:
- 17 August 2017, pp. 504-512
- Print publication:
- December 2017
-
- Article
-
- You have access
- Export citation
ON CONVEX COMBINATIONS OF CONVEX HARMONIC MAPPINGS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 96 / Issue 2 / October 2017
- Published online by Cambridge University Press:
- 07 August 2017, pp. 256-262
- Print publication:
- October 2017
-
- Article
-
- You have access
- Export citation
COEFFICIENT ESTIMATES FOR SOME CLASSES OF FUNCTIONS ASSOCIATED WITH
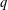 $q$ -FUNCTION THEORY
$q$ -FUNCTION THEORY
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 95 / Issue 3 / June 2017
- Published online by Cambridge University Press:
- 06 March 2017, pp. 446-456
- Print publication:
- June 2017
-
- Article
-
- You have access
- Export citation
A GENERALISATION OF THE CLUNIE–SHEIL-SMALL THEOREM II
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 95 / Issue 3 / June 2017
- Published online by Cambridge University Press:
- 02 March 2017, pp. 457-466
- Print publication:
- June 2017
-
- Article
-
- You have access
- Export citation
INVARIANCE OF THE COEFFICIENTS OF STRONGLY CONVEX FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 95 / Issue 3 / June 2017
- Published online by Cambridge University Press:
- 23 November 2016, pp. 436-445
- Print publication:
- June 2017
-
- Article
-
- You have access
- Export citation
LOGARITHMIC COEFFICIENTS OF SOME CLOSE-TO-CONVEX FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 95 / Issue 2 / April 2017
- Published online by Cambridge University Press:
- 02 November 2016, pp. 228-237
- Print publication:
- April 2017
-
- Article
-
- You have access
- Export citation
POLYGONAL QUASICONFORMAL MAPPINGS AND CHORD-ARC CURVES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 95 / Issue 1 / February 2017
- Published online by Cambridge University Press:
- 02 November 2016, pp. 66-72
- Print publication:
- February 2017
-
- Article
-
- You have access
- Export citation
Extremal Beltrami Differentials of Non-Landslide Type
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 60 / Issue 2 / May 2017
- Published online by Cambridge University Press:
- 25 October 2016, pp. 519-526
-
- Article
- Export citation
QUASICONFORMAL EXTENSIONS OF HARMONIC MAPPINGS WITH A COMPLEX PARAMETER
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 102 / Issue 3 / June 2017
- Published online by Cambridge University Press:
- 19 September 2016, pp. 307-315
- Print publication:
- June 2017
-
- Article
-
- You have access
- Export citation