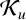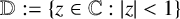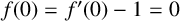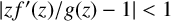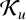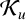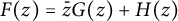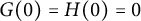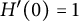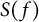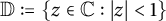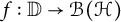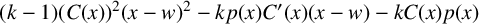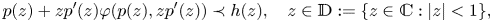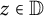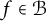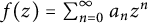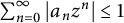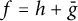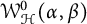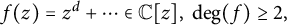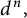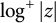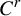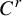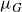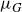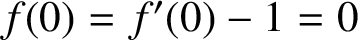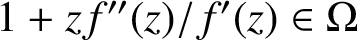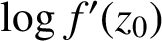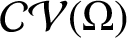Refine listing
Actions for selected content:
161 results in 30Cxx
Normal families and quasiregular mappings
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 23 October 2023, pp. 79-112
-
- Article
- Export citation
HARMONIC-MEASURE DISTRIBUTION FUNCTIONS AND RELATED FUNCTIONS FOR SIMPLY CONNECTED AND MULTIPLY CONNECTED TWO-DIMENSIONAL REGIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 06 October 2023, pp. 163-164
- Print publication:
- February 2024
-
- Article
-
- You have access
- HTML
- Export citation
ON CERTAIN CLOSE-TO-CONVEX FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 17 July 2023, pp. 365-375
- Print publication:
- April 2024
-
- Article
- Export citation
Landau-type theorems for certain bounded bi-analytic functions and biharmonic mappings
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 05 July 2023, pp. 152-165
- Print publication:
- March 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Bohr operator on operator-valued polyanalytic functions on simply connected domains
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 26 June 2023, pp. 1411-1422
- Print publication:
- December 2023
-
- Article
- Export citation
Refined Bohr inequalities for certain classes of functions: analytic, univalent, and convex
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 09 June 2023, pp. 9-25
- Print publication:
- March 2024
-
- Article
- Export citation
THE THIRD HANKEL DETERMINANT FOR INVERSE COEFFICIENTS OF CONVEX FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 02 May 2023, pp. 94-100
- Print publication:
- February 2024
-
- Article
- Export citation
ON THE NUMBER OF REAL ZEROS OF POLYNOMIALS OF EVEN DEGREE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 27 February 2023, pp. 89-93
- Print publication:
- February 2024
-
- Article
- Export citation
On a class of difference operator and its applications to a family of analytic functions
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 27 February 2023, pp. 248-258
- Print publication:
- February 2024
-
- Article
- Export citation
A new inner approach for differential subordinations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 10 February 2023, pp. 259-272
- Print publication:
- February 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Bohr–Rogosinski radius for a certain class of close-to-convex harmonic mappings
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 31 January 2023, pp. 1014-1029
- Print publication:
- September 2023
-
- Article
- Export citation
Mahler measure of polynomial iterates
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 12 January 2023, pp. 881-885
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Asymptotically holomorphic methods for infinitely renormalizable
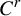 $C^r$ unimodal maps
$C^r$ unimodal maps
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 11 / November 2023
- Published online by Cambridge University Press:
- 29 November 2022, pp. 3636-3684
- Print publication:
- November 2023
-
- Article
- Export citation
Geometric versions of Schwarz’s lemma for spherically convex functions
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 6 / December 2023
- Published online by Cambridge University Press:
- 03 October 2022, pp. 1780-1799
- Print publication:
- December 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
An algebraic approach to a quartic analogue of the Kontsevich model
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 174 / Issue 3 / May 2023
- Published online by Cambridge University Press:
- 20 September 2022, pp. 471-495
- Print publication:
- May 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Zero and uniqueness sets for Fock spaces
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 25 July 2022, pp. 532-543
- Print publication:
- June 2023
-
- Article
- Export citation
Profiling ponded soil surface in saturated seepage into drain-line sink: Kalashnikov’s method of lateral leaching revisited
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 34 / Issue 2 / April 2023
- Published online by Cambridge University Press:
- 12 July 2022, pp. 367-384
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Conformally invariant complete metrics
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 174 / Issue 2 / March 2023
- Published online by Cambridge University Press:
- 30 May 2022, pp. 273-300
- Print publication:
- March 2023
-
- Article
- Export citation
On the roots of polynomials with log-convex coefficients
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 2 / April 2023
- Published online by Cambridge University Press:
- 15 February 2022, pp. 470-493
- Print publication:
- April 2023
-
- Article
- Export citation
AN APPLICATION OF SCHUR’S ALGORITHM TO VARIABILITY REGIONS OF CERTAIN ANALYTIC FUNCTIONS II
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 3 / June 2022
- Published online by Cambridge University Press:
- 02 December 2021, pp. 468-481
- Print publication:
- June 2022
-
- Article
- Export citation