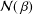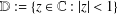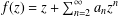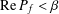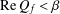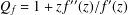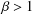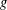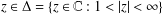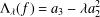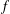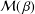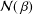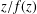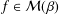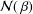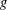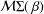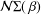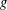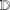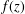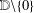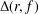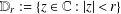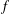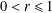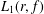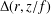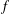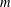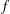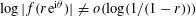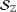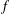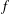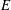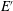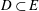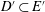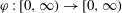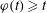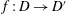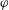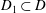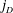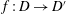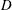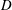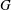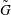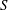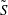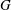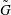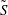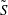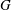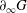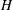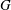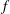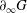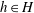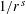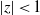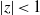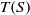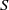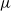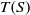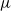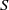Refine listing
Actions for selected content:
161 results in 30Cxx
NONDECREASABLE AND WEAKLY NONDECREASABLE DILATATIONS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 102 / Issue 3 / June 2017
- Published online by Cambridge University Press:
- 19 September 2016, pp. 420-434
- Print publication:
- June 2017
-
- Article
-
- You have access
- Export citation
RADII OF HARMONIC MAPPINGS IN THE PLANE
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 102 / Issue 3 / June 2017
- Published online by Cambridge University Press:
- 08 July 2016, pp. 331-347
- Print publication:
- June 2017
-
- Article
-
- You have access
- Export citation
Mappings of Lp-integrable distortion: regularity of the inverse
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 146 / Issue 3 / June 2016
- Published online by Cambridge University Press:
- 16 May 2016, pp. 647-663
- Print publication:
- June 2016
-
- Article
- Export citation
A Convexity Property of Discrete Random Walks
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 25 / Issue 6 / November 2016
- Published online by Cambridge University Press:
- 31 March 2016, pp. 928-940
-
- Article
- Export citation
ON THE EXISTENCE OF FINITE CRITICAL TRAJECTORIES IN A FAMILY OF QUADRATIC DIFFERENTIALS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 94 / Issue 1 / August 2016
- Published online by Cambridge University Press:
- 16 March 2016, pp. 80-91
- Print publication:
- August 2016
-
- Article
-
- You have access
- Export citation
A GENERALISATION OF THE CLUNIE–SHEIL-SMALL THEOREM
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 94 / Issue 1 / August 2016
- Published online by Cambridge University Press:
- 17 February 2016, pp. 92-100
- Print publication:
- August 2016
-
- Article
-
- You have access
- Export citation
COEFFICIENT INEQUALITIES AND YAMASHITA’S CONJECTURE FOR SOME CLASSES OF ANALYTIC FUNCTIONS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 100 / Issue 1 / February 2016
- Published online by Cambridge University Press:
- 29 September 2015, pp. 1-20
- Print publication:
- February 2016
-
- Article
-
- You have access
- Export citation
QUASICONFORMAL SOLUTIONS OF POISSON EQUATIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 92 / Issue 3 / December 2015
- Published online by Cambridge University Press:
- 19 August 2015, pp. 420-428
- Print publication:
- December 2015
-
- Article
-
- You have access
- Export citation
INTEGRAL MEANS AND DIRICHLET INTEGRAL FOR CERTAIN CLASSES OF ANALYTIC FUNCTIONS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 99 / Issue 3 / December 2015
- Published online by Cambridge University Press:
- 16 July 2015, pp. 315-333
- Print publication:
- December 2015
-
- Article
-
- You have access
- Export citation
UNIVALENT FUNCTIONS AND RADIAL GROWTH
- Part of
-
- Journal:
- Mathematika / Volume 61 / Issue 3 / September 2015
- Published online by Cambridge University Press:
- 16 January 2015, pp. 531-546
- Print publication:
- September 2015
-
- Article
- Export citation
CLASSIFICATION OF UNIVALENT HARMONIC MAPPINGS ON THE UNIT DISK WITH HALF-INTEGER COEFFICIENTS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 98 / Issue 2 / April 2015
- Published online by Cambridge University Press:
- 12 November 2014, pp. 257-280
- Print publication:
- April 2015
-
- Article
-
- You have access
- Export citation
FREELY QUASICONFORMAL MAPS AND DISTANCE RATIO METRIC
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 97 / Issue 3 / December 2014
- Published online by Cambridge University Press:
- 09 September 2014, pp. 383-390
- Print publication:
- December 2014
-
- Article
-
- You have access
- Export citation
Computing boundary extensions of conformal maps
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue 1 / 2014
- Published online by Cambridge University Press:
- 01 September 2014, pp. 360-378
-
- Article
-
- You have access
- Export citation
Local rigidity for hyperbolic groups with Sierpiński carpet boundaries
- Part of
-
- Journal:
- Compositio Mathematica / Volume 150 / Issue 11 / November 2014
- Published online by Cambridge University Press:
- 27 August 2014, pp. 1928-1938
- Print publication:
- November 2014
-
- Article
- Export citation
INVERSE BERNSTEIN INEQUALITIES AND MIN–MAX–MIN PROBLEMS ON THE UNIT CIRCLE
- Part of
-
- Journal:
- Mathematika / Volume 61 / Issue 3 / September 2015
- Published online by Cambridge University Press:
- 13 August 2014, pp. 581-590
- Print publication:
- September 2015
-
- Article
- Export citation
COEFFICIENT ESTIMATES, LANDAU’S THEOREM AND LIPSCHITZ-TYPE SPACES ON PLANAR HARMONIC MAPPINGS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 96 / Issue 2 / April 2014
- Published online by Cambridge University Press:
- 01 April 2014, pp. 198-215
- Print publication:
- April 2014
-
- Article
-
- You have access
- Export citation
SPECIAL CURVES AND POSTCRITICALLY FINITE POLYNOMIALS
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 1 / 2013
- Published online by Cambridge University Press:
- 19 September 2013, e3
-
- Article
-
- You have access
- Open access
- Export citation
REMARKS ON THE UNIVALENCE CRITERION OF PASCU AND PASCU
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 89 / Issue 2 / April 2014
- Published online by Cambridge University Press:
- 22 August 2013, pp. 210-216
- Print publication:
- April 2014
-
- Article
-
- You have access
- Export citation
DENSITY ESTIMATES ON COMPOSITE POLYNOMIALS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 95 / Issue 3 / December 2013
- Published online by Cambridge University Press:
- 07 August 2013, pp. 329-342
- Print publication:
- December 2013
-
- Article
-
- You have access
- Export citation
HAMILTON SEQUENCES FOR EXTREMAL QUASICONFORMAL MAPPINGS OF DOUBLY-CONNECTED DOMAINS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 88 / Issue 3 / December 2013
- Published online by Cambridge University Press:
- 22 March 2013, pp. 376-379
- Print publication:
- December 2013
-
- Article
-
- You have access
- Export citation

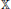 be an open set in ℝ
be an open set in ℝ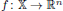 is a Sobolev homeomorphism. We study the regularity of
is a Sobolev homeomorphism. We study the regularity of