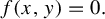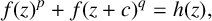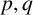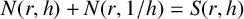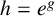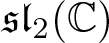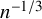Refine listing
Actions for selected content:
149 results in 30Dxx
On the rate of growth of random analytic functions, with an application to linear dynamics
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 28 August 2025, pp. 1-21
-
- Article
- Export citation
AN ASYMPTOTIC ESTIMATE FOR THE CHARACTERISTIC AND NUMBER OF FIXED POINTS OF THE RIEMANN ZETA FUNCTION
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 260 / December 2025
- Published online by Cambridge University Press:
- 01 August 2025, pp. 648-665
-
- Article
- Export citation
Semigroups of holomorphic functions; rectifiability and Lipschitz properties of the orbits
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 28 July 2025, pp. 1-30
-
- Article
- Export citation
A study of transcendental entire solutions of several nonlinear partial differential equations
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 68 / Issue 4 / November 2025
- Published online by Cambridge University Press:
- 22 July 2025, pp. 1329-1369
-
- Article
- Export citation
On an open problem of value sharing and differential equations
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 68 / Issue 4 / November 2025
- Published online by Cambridge University Press:
- 16 April 2025, pp. 1110-1136
-
- Article
- Export citation
On meromorphic solutions of certain partial differential equations
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 4 / December 2025
- Published online by Cambridge University Press:
- 24 March 2025, pp. 1177-1191
- Print publication:
- December 2025
-
- Article
- Export citation
A residue theorem for rational functions on star-shaped domains
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 17 February 2025, pp. 908-913
- Print publication:
- September 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Transcendental Julia sets of minimal Hausdorff dimension
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 8 / August 2025
- Published online by Cambridge University Press:
- 06 January 2025, pp. 2341-2413
- Print publication:
- August 2025
-
- Article
- Export citation
A note on Hayman’s problem
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 2 / June 2025
- Published online by Cambridge University Press:
- 18 December 2024, pp. 620-627
- Print publication:
- June 2025
-
- Article
- Export citation
Dynamics of projectable functions: towards an atlas of wandering domains for a family of Newton maps
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 25 November 2024, pp. 1-50
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Uniqueness theorems for meromorphic inner functions and canonical systems
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 25 November 2024, pp. 124-140
- Print publication:
- March 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Defect relation for holomorphic maps from complex discs into projective varieties and hypersurfaces
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 68 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 22 November 2024, pp. 157-172
-
- Article
- Export citation
On possible limit functions on a Fatou component in non-autonomous iteration
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 3 / March 2025
- Published online by Cambridge University Press:
- 28 October 2024, pp. 719-806
- Print publication:
- March 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On algebraic dependencies between Poincaré functions
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 3 / March 2025
- Published online by Cambridge University Press:
- 30 September 2024, pp. 915-935
- Print publication:
- March 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
NOTES ON FERMAT-TYPE DIFFERENCE EQUATIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 111 / Issue 2 / April 2025
- Published online by Cambridge University Press:
- 03 June 2024, pp. 324-335
- Print publication:
- April 2025
-
- Article
- Export citation
A classification of automorphic Lie algebras on complex tori
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 3 / August 2024
- Published online by Cambridge University Press:
- 28 May 2024, pp. 947-989
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A TROPICAL ANALOGUE OF THE LEMMA ON THE LOGARITHMIC DERIVATIVE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 110 / Issue 2 / October 2024
- Published online by Cambridge University Press:
- 20 May 2024, pp. 303-312
- Print publication:
- October 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Phase retrieval on circles and lines
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 10 May 2024, pp. 927-935
- Print publication:
- December 2024
-
- Article
- Export citation
Asymptotic expansions relating to the distribution of the length of longest increasing subsequences
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 15 March 2024, e36
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON THE ITERATIONS AND THE ARGUMENT DISTRIBUTION OF MEROMORPHIC FUNCTIONS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 116 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 15 February 2024, pp. 145-170
-
- Article
- Export citation























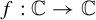
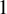



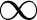
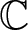
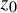

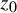
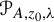 meromorphic on
meromorphic on 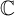
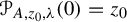 ,
, 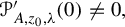 and
and 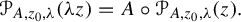 In this paper, we study the following problem: given Poincaré functions
In this paper, we study the following problem: given Poincaré functions 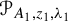 and
and 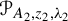 , find out if there is an algebraic relation
, find out if there is an algebraic relation 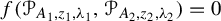 between them and, if such a relation exists, describe the corresponding algebraic curve
between them and, if such a relation exists, describe the corresponding algebraic curve