Refine listing
Actions for selected content:
47 results in 30Exx
Approximating the Riemann Zeta-function by Polynomials with Restricted Zeros
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 62 / Issue 3 / September 2019
- Published online by Cambridge University Press:
- 17 December 2018, pp. 475-478
- Print publication:
- September 2019
-
- Article
-
- You have access
- Export citation
Absolute continuity of distributions of one-dimensional Lévy processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 54 / Issue 3 / September 2017
- Published online by Cambridge University Press:
- 15 September 2017, pp. 852-872
- Print publication:
- September 2017
-
- Article
- Export citation
A Hybrid Spectral Element Method for Fractional Two-Point Boundary Value Problems
- Part of
-
- Journal:
- Numerical Mathematics: Theory, Methods and Applications / Volume 10 / Issue 2 / May 2017
- Published online by Cambridge University Press:
- 09 May 2017, pp. 437-464
- Print publication:
- May 2017
-
- Article
- Export citation
LIMITS OF FRACTIONAL DERIVATIVES AND COMPOSITIONS OF ANALYTIC FUNCTIONS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 103 / Issue 1 / August 2017
- Published online by Cambridge University Press:
- 28 September 2016, pp. 104-115
- Print publication:
- August 2017
-
- Article
-
- You have access
- Export citation
The Hele-Shaw flow and moduli of holomorphic discs
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 12 / December 2015
- Published online by Cambridge University Press:
- 18 August 2015, pp. 2301-2328
- Print publication:
- December 2015
-
- Article
- Export citation
A VERSION OF ROUCHÉ’S THEOREM FOR CONTINUOUS FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 91 / Issue 2 / April 2015
- Published online by Cambridge University Press:
- 09 December 2014, pp. 268-272
- Print publication:
- April 2015
-
- Article
-
- You have access
- Export citation
Computing boundary extensions of conformal maps
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue 1 / 2014
- Published online by Cambridge University Press:
- 01 September 2014, pp. 360-378
-
- Article
-
- You have access
- Export citation
EXTREME POINTS OF INTEGRAL FAMILIES OF ANALYTIC FUNCTIONS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 94 / Issue 2 / April 2013
- Published online by Cambridge University Press:
- 14 March 2013, pp. 202-221
- Print publication:
- April 2013
-
- Article
-
- You have access
- Export citation
Random Walks Reaching Against all Odds the other Side of the Quarter Plane
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 50 / Issue 1 / March 2013
- Published online by Cambridge University Press:
- 30 January 2018, pp. 85-102
- Print publication:
- March 2013
-
- Article
-
- You have access
- Export citation
Generalized ‘second Ritt theorem’ and explicit solution of the polynomial moment problem
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 4 / April 2013
- Published online by Cambridge University Press:
- 29 January 2013, pp. 705-728
- Print publication:
- April 2013
-
- Article
- Export citation
IRRATIONALITY AND NONQUADRATICITY MEASURES FOR LOGARITHMS OF ALGEBRAIC NUMBERS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 92 / Issue 2 / April 2012
- Published online by Cambridge University Press:
- 22 November 2012, pp. 237-267
- Print publication:
- April 2012
-
- Article
-
- You have access
- Export citation
NEIGHBOURHOODS OF UNIVALENT FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 83 / Issue 2 / April 2011
- Published online by Cambridge University Press:
- 14 September 2010, pp. 210-219
- Print publication:
- April 2011
-
- Article
-
- You have access
- Export citation
Analytic functions associated with strong Hamburger moment problems
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 52 / Issue 1 / February 2009
- Published online by Cambridge University Press:
- 02 February 2009, pp. 181-187
-
- Article
-
- You have access
- Export citation
REGULARITY OF CURVES WITH A CONTINUOUS TANGENT LINE
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 86 / Issue 1 / February 2009
- Published online by Cambridge University Press:
- 01 February 2009, pp. 17-26
- Print publication:
- February 2009
-
- Article
-
- You have access
- Export citation
Omitted rays and wedges of fractional Cauchy transforms
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 80 / Issue 3 / June 2006
- Published online by Cambridge University Press:
- 09 April 2009, pp. 367-373
- Print publication:
- June 2006
-
- Article
-
- You have access
- Export citation
U-Operators
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 78 / Issue 1 / February 2005
- Published online by Cambridge University Press:
- 09 April 2009, pp. 59-90
- Print publication:
- February 2005
-
- Article
-
- You have access
- Export citation
Analysis of generalized processor-sharing systems with two classes of customers and exponential services
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 41 / Issue 3 / September 2004
- Published online by Cambridge University Press:
- 14 July 2016, pp. 832-858
- Print publication:
- September 2004
-
- Article
- Export citation
Strongly omnipresent operators: general conditions and applications to composition operators
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 72 / Issue 3 / June 2002
- Published online by Cambridge University Press:
- 09 April 2009, pp. 335-348
- Print publication:
- June 2002
-
- Article
-
- You have access
- Export citation
On families of Cauchy transforms and BMOA
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 68 / Issue 3 / June 2000
- Published online by Cambridge University Press:
- 09 April 2009, pp. 357-364
- Print publication:
- June 2000
-
- Article
-
- You have access
- Export citation
Integral means on radially weighted spaces of analytic functions
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 65 / Issue 1 / August 1998
- Published online by Cambridge University Press:
- 09 April 2009, pp. 68-83
- Print publication:
- August 1998
-
- Article
-
- You have access
- Export citation
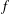
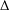
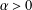
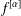
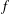
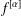
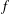

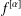
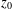
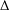
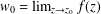
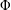
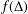
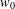
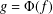
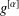
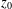
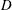
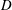
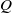
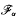
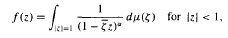 where μ is a complex-valued Borel measure on the unit circle. We show that if
where μ is a complex-valued Borel measure on the unit circle. We show that if 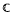 : |z| < 1} and there are two nonparallel rays in
: |z| < 1} and there are two nonparallel rays in 