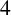 $4$
-MANIFOLDS
$4$
-MANIFOLDS
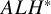 $ALH^*$
gravitational instantons
$ALH^*$
gravitational instantons
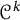 $\mathcal {C}^k$
-seeley-extension-theorem for Bastiani’s differential calculus
$\mathcal {C}^k$
-seeley-extension-theorem for Bastiani’s differential calculus
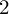 $2$
-SPHERES OF CONSTANT CURVATURE
$2$
-SPHERES OF CONSTANT CURVATURE