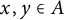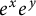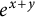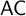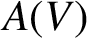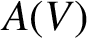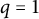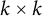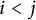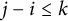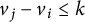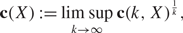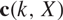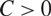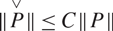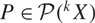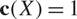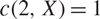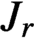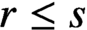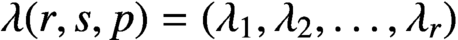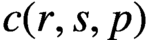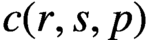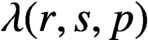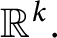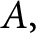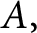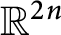Refine listing
Actions for selected content:
211 results in 15Axx
A refined nc Oka–Weil theorem
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 02 November 2021, pp. 218-224
- Print publication:
- March 2023
-
- Article
- Export citation
Commutativity via spectra of exponentials
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 02 November 2021, pp. 815-824
- Print publication:
- December 2022
-
- Article
- Export citation
ALMOST DISJOINT AND MAD FAMILIES IN VECTOR SPACES AND CHOICE PRINCIPLES
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 87 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 29 October 2021, pp. 1093-1110
- Print publication:
- September 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Non-negative integral matrices with given spectral radius and controlled dimension
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 10 / October 2022
- Published online by Cambridge University Press:
- 21 September 2021, pp. 3246-3269
- Print publication:
- October 2022
-
- Article
- Export citation
Hilbert’s 17th problem in free skew fields
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 06 September 2021, e61
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Spectral gap in random bipartite biregular graphs and applications
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 31 / Issue 2 / March 2022
- Published online by Cambridge University Press:
- 23 July 2021, pp. 229-267
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
STRUCTURED SINGULAR VALUES OF SOME GENERALISED STOCHASTIC MATRICES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 09 July 2021, pp. 58-67
- Print publication:
- February 2022
-
- Article
- Export citation
HERMITIANS IN MATRIX ALGEBRAS WITH OPERATOR NORM – II
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 64 / Issue 2 / May 2022
- Published online by Cambridge University Press:
- 10 June 2021, pp. 376-396
- Print publication:
- May 2022
-
- Article
- Export citation
HANKEL DETERMINANTS OF FACTORIAL FRACTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 07 June 2021, pp. 46-57
- Print publication:
- February 2022
-
- Article
- Export citation
Spectral distribution of symmetrized circulant matrices
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 03 June 2021, pp. 431-446
- Print publication:
- June 2022
-
- Article
- Export citation
INJECTIVE LINEAR TRANSFORMATIONS WITH EQUAL GAP AND DEFECT
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 18 May 2021, pp. 106-116
- Print publication:
- February 2022
-
- Article
- Export citation
DETERMINANTS AND PERMANENTS OF POWER MATRICES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 17 May 2021, pp. 37-45
- Print publication:
- February 2022
-
- Article
- Export citation
1324- and 2143-avoiding Kazhdan–Lusztig immanants and k-positivity
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 14 May 2021, pp. 52-82
- Print publication:
- February 2023
-
- Article
- Export citation
The polarization constant of finite dimensional complex spaces is one
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 172 / Issue 1 / January 2022
- Published online by Cambridge University Press:
- 04 March 2021, pp. 105-123
- Print publication:
- January 2022
-
- Article
- Export citation
Some matrix inequalities of log-majorization type
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 1 / March 2022
- Published online by Cambridge University Press:
- 26 February 2021, pp. 95-105
- Print publication:
- March 2022
-
- Article
- Export citation
NONNEGATIVE POLYNOMIALS, SUMS OF SQUARES AND THE MOMENT PROBLEM
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 104 / Issue 2 / October 2021
- Published online by Cambridge University Press:
- 19 February 2021, pp. 337-341
- Print publication:
- October 2021
-
- Article
-
- You have access
- Export citation
A NEW ALGORITHM FOR DECOMPOSING MODULAR TENSOR PRODUCTS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 104 / Issue 1 / August 2021
- Published online by Cambridge University Press:
- 11 January 2021, pp. 94-107
- Print publication:
- August 2021
-
- Article
- Export citation
Tight frames and related geometric problems
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 18 December 2020, pp. 942-963
- Print publication:
- December 2021
-
- Article
- Export citation
Inequalities on partial traces of positive semidefinite block matrices
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 18 December 2020, pp. 964-969
- Print publication:
- December 2021
-
- Article
- Export citation
Derivatives of symplectic eigenvalues and a Lidskii type theorem
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 74 / Issue 2 / April 2022
- Published online by Cambridge University Press:
- 02 December 2020, pp. 457-485
- Print publication:
- April 2022
-
- Article
-
- You have access
- Export citation