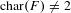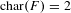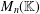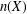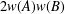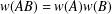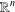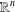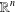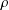Refine listing
Actions for selected content:
211 results in 15Axx
Jordan–Chevalley Decomposition in Lie Algebras
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 62 / Issue 2 / June 2019
- Published online by Cambridge University Press:
- 28 February 2019, pp. 349-354
- Print publication:
- June 2019
-
- Article
-
- You have access
- Export citation
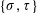 $\{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70F}\}$-Rota–Baxter Operators, Infinitesimal Hom-bialgebras and the Associative (Bi)Hom-Yang–Baxter Equation
$\{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70F}\}$-Rota–Baxter Operators, Infinitesimal Hom-bialgebras and the Associative (Bi)Hom-Yang–Baxter Equation
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 62 / Issue 2 / June 2019
- Published online by Cambridge University Press:
- 07 January 2019, pp. 355-372
- Print publication:
- June 2019
-
- Article
-
- You have access
- Export citation
ON MINIMAL SETS OF
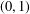 $(0,1)$ -MATRICES WHOSE PAIRWISE PRODUCTS FORM A BASIS FOR
$(0,1)$ -MATRICES WHOSE PAIRWISE PRODUCTS FORM A BASIS FOR 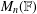 $M_{n}(\mathbb{F})$
$M_{n}(\mathbb{F})$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 98 / Issue 3 / December 2018
- Published online by Cambridge University Press:
- 28 August 2018, pp. 402-413
- Print publication:
- December 2018
-
- Article
-
- You have access
- Export citation
A STRUCTURED INVERSE SPECTRUM PROBLEM FOR INFINITE GRAPHS ANDUNBOUNDED OPERATORS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 98 / Issue 3 / December 2018
- Published online by Cambridge University Press:
- 15 August 2018, pp. 363-371
- Print publication:
- December 2018
-
- Article
-
- You have access
- Export citation
RELATIVE PERTURBATION BOUNDS FOR THE JOINT SPECTRUM OF COMMUTINGTUPLES OF MATRICES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 98 / Issue 3 / December 2018
- Published online by Cambridge University Press:
- 05 July 2018, pp. 414-421
- Print publication:
- December 2018
-
- Article
-
- You have access
- Export citation
TRANSFORMATIONS ON DENSITY OPERATORS PRESERVING GENERALISED ENTROPY OF A CONVEX COMBINATION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 98 / Issue 1 / August 2018
- Published online by Cambridge University Press:
- 03 May 2018, pp. 102-108
- Print publication:
- August 2018
-
- Article
-
- You have access
- Export citation
Perforation conditions and almost algebraic order in Cuntz semigroups
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 148 / Issue 4 / August 2018
- Published online by Cambridge University Press:
- 18 April 2018, pp. 669-702
- Print publication:
- August 2018
-
- Article
- Export citation
A BOUND FOR THE INDEX OF A QUADRATIC FORM AFTER SCALAR EXTENSION TO THE FUNCTION FIELD OF A QUADRIC
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 2 / March 2020
- Published online by Cambridge University Press:
- 16 April 2018, pp. 421-450
- Print publication:
- March 2020
-
- Article
- Export citation
GRASSMANNIAN SEMIGROUPS AND THEIR REPRESENTATIONS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 104 / Issue 3 / June 2018
- Published online by Cambridge University Press:
- 27 March 2018, pp. 308-337
- Print publication:
- June 2018
-
- Article
-
- You have access
- Export citation
Sums of Quadratic Endomorphisms of an Infinite-Dimensional Vector Space
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 61 / Issue 2 / May 2018
- Published online by Cambridge University Press:
- 26 February 2018, pp. 437-447
-
- Article
- Export citation
IMPROVED INEQUALITIES FOR THE NUMERICAL RADIUS: WHEN INVERSE COMMUTES WITH THE NORM
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 97 / Issue 2 / April 2018
- Published online by Cambridge University Press:
- 02 February 2018, pp. 293-296
- Print publication:
- April 2018
-
- Article
-
- You have access
- Export citation
POTENTIALS OF A FROBENIUS-LIKE STRUCTURE
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 60 / Issue 3 / September 2018
- Published online by Cambridge University Press:
- 28 January 2018, pp. 681-693
- Print publication:
- September 2018
-
- Article
-
- You have access
- Export citation
A NOTE ON COMPUTING THE INTERSECTION OF SPHERES IN
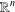 $\mathbb{R}^{n}$
$\mathbb{R}^{n}$
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 59 / Issue 2 / October 2017
- Published online by Cambridge University Press:
- 02 November 2017, pp. 271-279
-
- Article
-
- You have access
- Export citation
PRODUCTS OF ROTATIONS BY A GIVEN ANGLE IN THE ORTHOGONAL GROUP
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 97 / Issue 2 / April 2018
- Published online by Cambridge University Press:
- 02 November 2017, pp. 308-312
- Print publication:
- April 2018
-
- Article
-
- You have access
- Export citation
Solution of a Nonlinear Eigenvalue Problem Using Signed Singular Values
- Part of
-
- Journal:
- East Asian Journal on Applied Mathematics / Volume 7 / Issue 4 / November 2017
- Published online by Cambridge University Press:
- 31 January 2018, pp. 799-809
- Print publication:
- November 2017
-
- Article
- Export citation
Integrable Properties of a Variant of the Discrete Hungry Toda Equations and Their Relationship to Eigenpairs of Band Matrices
- Part of
-
- Journal:
- East Asian Journal on Applied Mathematics / Volume 7 / Issue 4 / November 2017
- Published online by Cambridge University Press:
- 31 January 2018, pp. 785-798
- Print publication:
- November 2017
-
- Article
- Export citation
Efficient Preconditioner and Iterative Method for Large Complex Symmetric Linear Algebraic Systems
- Part of
-
- Journal:
- East Asian Journal on Applied Mathematics / Volume 7 / Issue 3 / August 2017
- Published online by Cambridge University Press:
- 07 September 2017, pp. 530-547
- Print publication:
- August 2017
-
- Article
- Export citation
Analysis of Hexagonal Grid Finite Difference Methods for Anisotropic Laplacian Related Equations
- Part of
-
- Journal:
- Numerical Mathematics: Theory, Methods and Applications / Volume 10 / Issue 3 / August 2017
- Published online by Cambridge University Press:
- 20 June 2017, pp. 562-596
- Print publication:
- August 2017
-
- Article
- Export citation
Numerical Ranges in II1 Factors
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 61 / Issue 1 / February 2018
- Published online by Cambridge University Press:
- 16 March 2017, pp. 31-55
-
- Article
- Export citation
The Disc Theorem for the Schur Complement of Two Class Submatrices with γ-Diagonally Dominant Properties
- Part of
-
- Journal:
- Numerical Mathematics: Theory, Methods and Applications / Volume 10 / Issue 1 / February 2017
- Published online by Cambridge University Press:
- 20 February 2017, pp. 84-97
- Print publication:
- February 2017
-
- Article
- Export citation


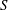
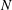
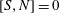
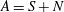
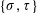
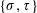
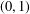
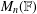
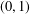
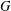
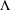
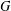
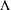
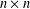
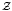 ) in terms of Cu(
) in terms of Cu(