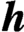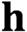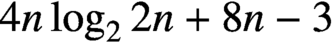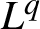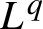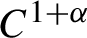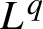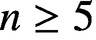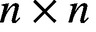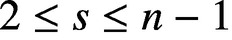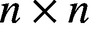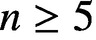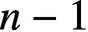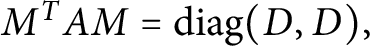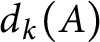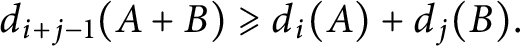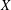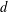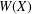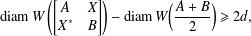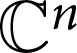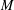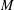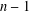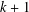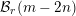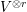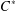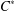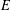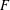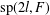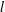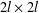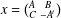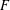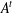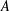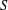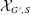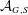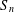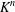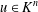Refine listing
Actions for selected content:
211 results in 15Axx
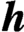 $\textit{h}$-MINIMUM SPANNING LENGTHS AND AN EXTENSION TO BURNSIDE’S THEOREM ON IRREDUCIBILITY
$\textit{h}$-MINIMUM SPANNING LENGTHS AND AN EXTENSION TO BURNSIDE’S THEOREM ON IRREDUCIBILITY
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 104 / Issue 1 / August 2021
- Published online by Cambridge University Press:
- 02 December 2020, pp. 78-93
- Print publication:
- August 2021
-
- Article
- Export citation
MULTINOMIAL VANDERMONDE CONVOLUTION VIA PERMANENT
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 103 / Issue 3 / June 2021
- Published online by Cambridge University Press:
- 06 November 2020, pp. 353-361
- Print publication:
- June 2021
-
- Article
- Export citation
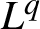 $L^{q}$-spectra of measures on planar non-conformal attractors
$L^{q}$-spectra of measures on planar non-conformal attractors
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 11 / November 2021
- Published online by Cambridge University Press:
- 26 October 2020, pp. 3288-3306
- Print publication:
- November 2021
-
- Article
- Export citation
THE SLOT LENGTH OF A FAMILY OF MATRICES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 103 / Issue 2 / April 2021
- Published online by Cambridge University Press:
- 05 October 2020, pp. 260-270
- Print publication:
- April 2021
-
- Article
- Export citation
Lineability, continuity, and antiderivatives in the non-Archimedean setting
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 02 September 2020, pp. 638-650
- Print publication:
- September 2021
-
- Article
- Export citation
Variational principles for symplectic eigenvalues
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 20 August 2020, pp. 553-559
- Print publication:
- September 2021
-
- Article
- Export citation
NUMERICAL RANGE AND POSITIVE BLOCK MATRICES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 103 / Issue 1 / February 2021
- Published online by Cambridge University Press:
- 11 June 2020, pp. 69-77
- Print publication:
- February 2021
-
- Article
- Export citation
HERMITIANS IN MATRIX ALGEBRAS WITH OPERATOR NORM
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 63 / Issue 2 / May 2021
- Published online by Cambridge University Press:
- 27 April 2020, pp. 280-290
- Print publication:
- May 2021
-
- Article
- Export citation
The Distance from a Rank
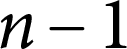 $n-1$ Projection to the Nilpotent Operators on
$n-1$ Projection to the Nilpotent Operators on 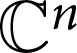 $\mathbb {C}^n$
$\mathbb {C}^n$
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 1 / March 2021
- Published online by Cambridge University Press:
- 02 April 2020, pp. 54-74
- Print publication:
- March 2021
-
- Article
- Export citation
IRREDUCIBLE FAMILIES OF COMPLEX MATRICES CONTAINING A RANK-ONE MATRIX
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 102 / Issue 2 / October 2020
- Published online by Cambridge University Press:
- 16 January 2020, pp. 226-236
- Print publication:
- October 2020
-
- Article
-
- You have access
- Export citation
INEQUALITIES OF JENSEN’S TYPE FOR POSITIVE LINEAR FUNCTIONALS ON HERMITIAN UNITAL BANACH
 $\ast$-ALGEBRAS
$\ast$-ALGEBRAS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 102 / Issue 2 / October 2020
- Published online by Cambridge University Press:
- 08 January 2020, pp. 308-318
- Print publication:
- October 2020
-
- Article
-
- You have access
- Export citation
THE SECOND FUNDAMENTAL THEOREM OF INVARIANT THEORY FOR THE ORTHOSYMPLECTIC SUPERGROUP
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 242 / June 2021
- Published online by Cambridge University Press:
- 04 December 2019, pp. 52-76
- Print publication:
- June 2021
-
- Article
- Export citation
Products of Involutions of an Infinite-dimensional Vector Space
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 73 / Issue 1 / February 2021
- Published online by Cambridge University Press:
- 15 November 2019, pp. 195-220
- Print publication:
- February 2021
-
- Article
- Export citation
WEIGHTED CORE–EP INVERSE AND WEIGHTED CORE–EP PRE-ORDERS IN A
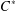 $C^{\ast }$-ALGEBRA
$C^{\ast }$-ALGEBRA
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 111 / Issue 1 / August 2021
- Published online by Cambridge University Press:
- 18 October 2019, pp. 76-110
- Print publication:
- August 2021
-
- Article
- Export citation
Triangularization of Matrices and Polynomial Maps
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 63 / Issue 1 / March 2020
- Published online by Cambridge University Press:
- 18 September 2019, pp. 94-105
- Print publication:
- March 2020
-
- Article
-
- You have access
- Export citation
Poincaré duality and resonance varieties
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 6 / December 2020
- Published online by Cambridge University Press:
- 13 September 2019, pp. 3001-3027
- Print publication:
- December 2020
-
- Article
- Export citation
ON A FUNCTION MODULE WITH APPROXIMATE HYPERPLANE SERIES PROPERTY
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 108 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 03 July 2019, pp. 341-348
- Print publication:
- June 2020
-
- Article
-
- You have access
- Export citation
DIAMETER OF COMMUTING GRAPHS OF SYMPLECTIC ALGEBRAS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 100 / Issue 3 / December 2019
- Published online by Cambridge University Press:
- 04 June 2019, pp. 419-427
- Print publication:
- December 2019
-
- Article
-
- You have access
- Export citation
CLUSTER STRUCTURES ON HIGHER TEICHMULLER SPACES FOR CLASSICAL GROUPS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 7 / 2019
- Published online by Cambridge University Press:
- 08 May 2019, e13
-
- Article
-
- You have access
- Open access
- Export citation
ON THE DIMENSION OF PERMUTATION VECTOR SPACES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 100 / Issue 2 / October 2019
- Published online by Cambridge University Press:
- 03 April 2019, pp. 256-267
- Print publication:
- October 2019
-
- Article
-
- You have access
- Export citation