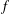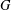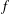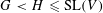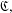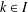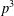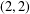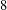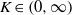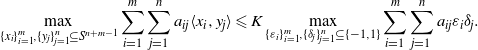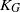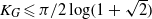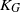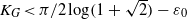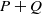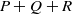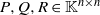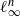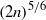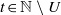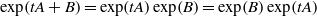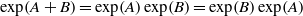Refine listing
Actions for selected content:
211 results in 15Axx
SIMPLE GROUPS STABILIZING POLYNOMIALS
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 3 / 2015
- Published online by Cambridge University Press:
- 15 June 2015, e3
-
- Article
-
- You have access
- Open access
- Export citation
On the derived category of Grassmannians in arbitrary characteristic
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 7 / July 2015
- Published online by Cambridge University Press:
- 15 April 2015, pp. 1242-1264
- Print publication:
- July 2015
-
- Article
- Export citation
ON DIFFERENCES BETWEEN THE BORDER RANK AND THE SMOOTHABLE RANK OF A POLYNOMIAL
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 57 / Issue 2 / May 2015
- Published online by Cambridge University Press:
- 17 December 2014, pp. 401-413
- Print publication:
- May 2015
-
- Article
-
- You have access
- Export citation
(ANTI)COMMUTATIVE ALGEBRAS WITH A MULTIPLICATIVE BASIS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 91 / Issue 2 / April 2015
- Published online by Cambridge University Press:
- 15 December 2014, pp. 211-218
- Print publication:
- April 2015
-
- Article
-
- You have access
- Export citation
THE CLASS OF (2, 2)-GROUPS WITH HOMOCYCLIC REGULATOR QUOTIENT OF EXPONENT
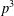 $p^{3}$ HAS BOUNDED REPRESENTATION TYPE
$p^{3}$ HAS BOUNDED REPRESENTATION TYPE
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 99 / Issue 1 / August 2015
- Published online by Cambridge University Press:
- 04 December 2014, pp. 12-29
- Print publication:
- August 2015
-
- Article
-
- You have access
- Export citation
LINEAR MAPS PRESERVING TENSOR PRODUCTS OF RANK-ONE HERMITIAN MATRICES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 98 / Issue 3 / June 2015
- Published online by Cambridge University Press:
- 21 November 2014, pp. 407-428
- Print publication:
- June 2015
-
- Article
-
- You have access
- Export citation
Improved Approximation of the Sum of Random Vectors by the Skew Normal Distribution
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 51 / Issue 2 / June 2014
- Published online by Cambridge University Press:
- 19 February 2016, pp. 466-482
- Print publication:
- June 2014
-
- Article
-
- You have access
- Export citation
A New Look at Urban Water Storage in a Series of Connected Dams
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 51 / Issue 1 / March 2014
- Published online by Cambridge University Press:
- 30 January 2018, pp. 118-135
- Print publication:
- March 2014
-
- Article
-
- You have access
- Export citation
On the Embedding Problem for Discrete-Time Markov Chains
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 50 / Issue 4 / December 2013
- Published online by Cambridge University Press:
- 30 January 2018, pp. 918-930
- Print publication:
- December 2013
-
- Article
-
- You have access
- Export citation
THE GROTHENDIECK CONSTANT IS STRICTLY SMALLER THAN KRIVINE’S BOUND
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 1 / 2013
- Published online by Cambridge University Press:
- 19 November 2013, e4
-
- Article
-
- You have access
- Open access
- Export citation
ON THE GROUP INVERSE FOR THE SUM OF MATRICES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 96 / Issue 1 / February 2014
- Published online by Cambridge University Press:
- 08 November 2013, pp. 36-43
- Print publication:
- February 2014
-
- Article
-
- You have access
- Export citation
SYMMETRIC ALGEBRAS OVER RINGS AND FIELDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 89 / Issue 3 / June 2014
- Published online by Cambridge University Press:
- 06 September 2013, pp. 466-472
- Print publication:
- June 2014
-
- Article
-
- You have access
- Export citation
RESTRICTED INVERTIBILITY AND THE BANACH–MAZUR DISTANCE TO THE CUBE
- Part of
-
- Journal:
- Mathematika / Volume 60 / Issue 1 / January 2014
- Published online by Cambridge University Press:
- 02 September 2013, pp. 201-218
- Print publication:
- January 2014
-
- Article
- Export citation
DENSITY ESTIMATES ON COMPOSITE POLYNOMIALS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 95 / Issue 3 / December 2013
- Published online by Cambridge University Press:
- 07 August 2013, pp. 329-342
- Print publication:
- December 2013
-
- Article
-
- You have access
- Export citation
Eigenvalues of Hermitian matrices and equivariant cohomology of Grassmannians
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 9 / September 2013
- Published online by Cambridge University Press:
- 07 August 2013, pp. 1569-1582
- Print publication:
- September 2013
-
- Article
- Export citation
PROPERTY L AND COMMUTING EXPONENTIALS IN DIMENSION AT MOST THREE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 89 / Issue 1 / February 2014
- Published online by Cambridge University Press:
- 28 June 2013, pp. 70-78
- Print publication:
- February 2014
-
- Article
-
- You have access
- Export citation
Cross-Commodity Spot Price Modeling with Stochastic Volatility and Leverage For Energy Markets
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 45 / Issue 2 / June 2013
- Published online by Cambridge University Press:
- 22 February 2016, pp. 545-571
- Print publication:
- June 2013
-
- Article
-
- You have access
- Export citation
Pricing of Forwards and Options in a Multivariate Non-Gaussian Stochastic Volatility Model for Energy Markets
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 45 / Issue 2 / June 2013
- Published online by Cambridge University Press:
- 22 February 2016, pp. 572-594
- Print publication:
- June 2013
-
- Article
-
- You have access
- Export citation
TRACE INEQUALITIES AND A QUESTION OF BOURIN
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 88 / Issue 3 / December 2013
- Published online by Cambridge University Press:
- 25 January 2013, pp. 384-389
- Print publication:
- December 2013
-
- Article
-
- You have access
- Export citation
Rational maps between quasilinear hypersurfaces
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 3 / March 2013
- Published online by Cambridge University Press:
- 17 December 2012, pp. 333-355
- Print publication:
- March 2013
-
- Article
- Export citation