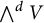Refine listing
Actions for selected content:
211 results in 15Axx
Linear damping estimates for periodic roll wave solutions of the inviscid Saint-Venant equations and related systems of hyperbolic balance laws
- Part of
-
- Journal:
- Journal of Nonlinear Waves / Volume 1 / 2025
- Published online by Cambridge University Press:
- 05 December 2025, e21
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A NEW PROOF OF THE SINGULAR CONTINUITY OF THE MINKOWSKI
 $?$-FUNCTION
$?$-FUNCTION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 04 December 2025, pp. 1-6
-
- Article
- Export citation
Polynomial invariants for three-dimensional Leibniz algebras
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 25 November 2025, pp. 1-20
-
- Article
- Export citation
Cartan decomposition for
 $\mathrm {Sp}(1,n)$ and some applications to group dynamics
$\mathrm {Sp}(1,n)$ and some applications to group dynamics
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 28 October 2025, pp. 1-17
-
- Article
- Export citation
A classification of
 $\mathbb {Q}$-linear maps from
$\mathbb {Q}$-linear maps from  $\overline {\mathbb {Q}}^\times /\overline {\mathbb {Q}}^\times _{\mathrm {tors}}$ to
$\overline {\mathbb {Q}}^\times /\overline {\mathbb {Q}}^\times _{\mathrm {tors}}$ to  $\mathbb {R}$
$\mathbb {R}$
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 21 October 2025, pp. 1-19
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Tunable localisation in parity-time-symmetric resonator arrays with imaginary gauge potentials
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 26 September 2025, e157
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Groups of matrices with approximately submultiplicative spectra
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 16 September 2025, pp. 1-11
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Orthogonal matroids over tracts
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 05 August 2025, e130
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the edge eigenvalues of the precision matrices of nonstationary autoregressive processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 57 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 27 May 2025, pp. 907-939
- Print publication:
- September 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A tensor restriction theorem over finite fields
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 5 / May 2025
- Published online by Cambridge University Press:
- 29 August 2025, pp. 1021-1053
- Print publication:
- May 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Strongly reversible classes in SL(n, ℂ)
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 68 / Issue 4 / November 2025
- Published online by Cambridge University Press:
- 30 April 2025, pp. 1137-1168
-
- Article
- Export citation
Topological Noetherianity of the infinite half-spin representations
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 21 April 2025, e75
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On exterior powers of reflection representations, II
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 24 March 2025, pp. 1-23
-
- Article
- Export citation
Generalized Knill–Laflamme theorem for families of isoclinic subspaces
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 17 March 2025, pp. 992-1010
- Print publication:
- September 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A non-convex optimization approach of searching algebraic degree phase-type representations for general phase-type distributions
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 57 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 03 March 2025, pp. 1101-1137
- Print publication:
- September 2025
-
- Article
- Export citation
The algebraic numerical range as a spectral set in Banach algebras
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 17 February 2025, pp. 1-25
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Right-angled Artin groups and the cohomology basis graph
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 68 / Issue 2 / May 2025
- Published online by Cambridge University Press:
- 03 February 2025, pp. 634-654
-
- Article
- Export citation
Products of commutators in matrix rings
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 2 / June 2025
- Published online by Cambridge University Press:
- 14 January 2025, pp. 512-529
- Print publication:
- June 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Product of two involutions in quaternionic special linear group
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 2 / June 2025
- Published online by Cambridge University Press:
- 08 January 2025, pp. 421-439
- Print publication:
- June 2025
-
- Article
- Export citation
The Markov chain embedding problem in a one-jump setting
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 62 / Issue 2 / June 2025
- Published online by Cambridge University Press:
- 09 December 2024, pp. 674-696
- Print publication:
- June 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation