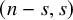Refine listing
Actions for selected content:
545 results in 11Gxx
COHOMOLOGY OF THE BASIC UNRAMIFIED PEL UNITARY RAPOPORT-ZINK SPACE OF SIGNATURE
 $(1,n-1)$
$(1,n-1)$
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu , First View
- Published online by Cambridge University Press:
- 18 December 2025, pp. 1-59
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Likely intersections
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 15 December 2025, e199
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
GENERALISED MAZUR’S GROWTH NUMBER CONJECTURE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 28 November 2025, pp. 1-16
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
An asymptotic formula for Tate–Shafarevich groups of CM elliptic curves at supersingular primes
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 13 November 2025, pp. 1-15
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
NON-SEMI-STABLE LOCI IN HECKE STACKS AND FARGUES’ CONJECTURE
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu , First View
- Published online by Cambridge University Press:
- 23 October 2025, pp. 1-31
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A classification of
 $\mathbb {Q}$-linear maps from
$\mathbb {Q}$-linear maps from  $\overline {\mathbb {Q}}^\times /\overline {\mathbb {Q}}^\times _{\mathrm {tors}}$ to
$\overline {\mathbb {Q}}^\times /\overline {\mathbb {Q}}^\times _{\mathrm {tors}}$ to  $\mathbb {R}$
$\mathbb {R}$
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 21 October 2025, pp. 1-19
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON INTEGRAL LOCAL SHIMURA VARIETIES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu , First View
- Published online by Cambridge University Press:
- 14 October 2025, pp. 1-69
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the weak Harder–Narasimhan stratification on
 $B_{\mathrm{dR}}^+$-affine Grassmannian
$B_{\mathrm{dR}}^+$-affine Grassmannian
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 10 / October 2025
- Published online by Cambridge University Press:
- 15 December 2025, pp. 2654-2711
- Print publication:
- October 2025
-
- Article
- Export citation
Rigid meromorphic cocycles for orthogonal groups
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 30 September 2025, e160
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Anisotropic area-preserving flows for plane curves and entropy inequalities
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 23 September 2025, pp. 1-25
-
- Article
- Export citation
Improvements on dimension growth results and effective Hilbert’s irreducibility theorem
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 19 September 2025, e153
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
HODGE CYCLES AND QUADRATIC RELATIONS BETWEEN HOLOMORPHIC PERIODS ON CM ABELIAN VARIETIES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu , First View
- Published online by Cambridge University Press:
- 19 September 2025, pp. 1-35
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On (2,2)-decomposable genus 4 Jacobians
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 12 September 2025, pp. 1-26
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Improved bounds for Serre’s open image theorem
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 10 September 2025, pp. 1-19
-
- Article
- Export citation
F-zips with additional structure on splitting models of Shimura varieties
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 09 September 2025, e142
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Arithmetic Transfer for inner forms of
 $GL_{2n}$
$GL_{2n}$
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 04 August 2025, e128
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Semi-stable and splitting models for unitary Shimura varieties over ramified places. I.
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 17 July 2025, e119
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the Fitting ideals of anticyclotomic Selmer groups of elliptic curves with good ordinary reduction
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 14 July 2025, pp. 1-11
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Elliptic curves and spin
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 179 / Issue 3 / November 2025
- Published online by Cambridge University Press:
- 11 July 2025, pp. 519-539
- Print publication:
- November 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Modularity of arithmetic special divisors for unitary Shimura varieties (with an appendix by Yujie Xu)
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 10 July 2025, e111
-
- Article
-
- You have access
- Open access
- HTML
- Export citation

























 .
.