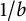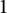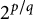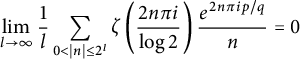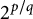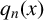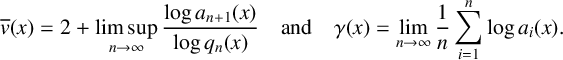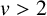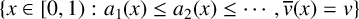Refine listing
Actions for selected content:
187 results in 11Kxx
Disintegration results for fractal measures and applications to Diophantine approximation
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems , First View
- Published online by Cambridge University Press:
- 23 December 2025, pp. 1-18
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A threshold for Poisson behavior of non-stationary product measures
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems , First View
- Published online by Cambridge University Press:
- 04 December 2025, pp. 1-11
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The structure of Lonely Runner spectra
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society , First View
- Published online by Cambridge University Press:
- 24 October 2025, pp. 1-19
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A new class of α-Farey maps and an application to normal numbers
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 15 September 2025, pp. 1-37
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Asymptotic behavior for the sum of partial quotients in continued fraction expansions
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 11 September 2025, pp. 1-13
-
- Article
- Export citation
Equidistribution in the complex plane and self-similar measures
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 09 September 2025, pp. 1-27
-
- Article
- Export citation
METRICAL PROPERTIES OF CONTINUED FRACTION AND LÜROTH SERIES EXPANSIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 112 / Issue 3 / December 2025
- Published online by Cambridge University Press:
- 04 September 2025, pp. 563-567
- Print publication:
- December 2025
-
- Article
-
- You have access
- HTML
- Export citation
Moments of random multiplicative functions over function fields
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 179 / Issue 3 / November 2025
- Published online by Cambridge University Press:
- 08 August 2025, pp. 785-819
- Print publication:
- November 2025
-
- Article
- Export citation
Ergodicity and algebraicity of the fast and slow triangle maps
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 46 / Issue 1 / January 2026
- Published online by Cambridge University Press:
- 08 August 2025, pp. 93-127
- Print publication:
- January 2026
-
- Article
- Export citation
On Dirichlet non-improvable numbers and shrinking target problems
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 11 / November 2025
- Published online by Cambridge University Press:
- 11 June 2025, pp. 3540-3568
- Print publication:
- November 2025
-
- Article
- Export citation
A criterion for the simple normality of fractional powers of two via the Riemann zeta function
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 29 May 2025, pp. 1-24
-
- Article
- Export citation
Almost sure upper bound for a model problem for multiplicative chaos in number theory
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 179 / Issue 1 / July 2025
- Published online by Cambridge University Press:
- 13 May 2025, pp. 29-44
- Print publication:
- July 2025
-
- Article
- Export citation
On inhomogeneous Poissonian pair correlations
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 179 / Issue 1 / July 2025
- Published online by Cambridge University Press:
- 13 May 2025, pp. 17-27
- Print publication:
- July 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A NOTE ON CHARACTER SUMS OVER SHORT MOVING INTERVALS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 4 / July 2025
- Published online by Cambridge University Press:
- 13 February 2025, pp. 1395-1427
- Print publication:
- July 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Furstenberg systems of pretentious and MRT multiplicative functions
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 9 / September 2025
- Published online by Cambridge University Press:
- 03 February 2025, pp. 2765-2844
- Print publication:
- September 2025
-
- Article
- Export citation
Small Mahler measures with bounds on the house and shortness
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 2 / June 2025
- Published online by Cambridge University Press:
- 20 January 2025, pp. 603-619
- Print publication:
- June 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Zero-full law for well approximable sets in missing digit sets
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 178 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 20 February 2025, pp. 81-102
- Print publication:
- January 2025
-
- Article
- Export citation
Full Poissonian local statistics of slowly growing sequences
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 24 March 2025, pp. 148-180
- Print publication:
- January 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Birkhoff spectrum for diagonally self-affine sets and digit frequencies for GLS systems with redundancy
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 09 December 2024, pp. 1-26
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
THE MULTIFRACTAL SPECTRUM OF CONTINUED FRACTIONS WITH NONDECREASING PARTIAL QUOTIENTS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 112 / Issue 1 / August 2025
- Published online by Cambridge University Press:
- 25 November 2024, pp. 93-105
- Print publication:
- August 2025
-
- Article
- Export citation