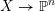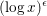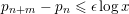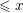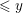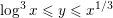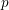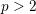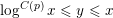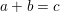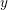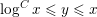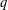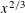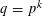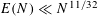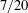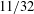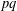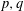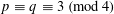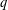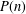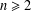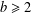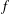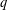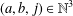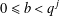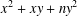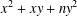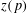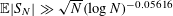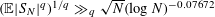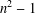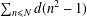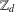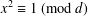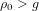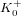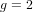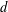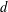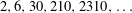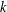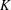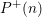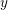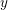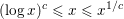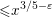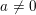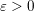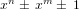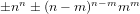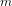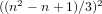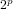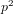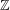Refine listing
Actions for selected content:
286 results in 11Nxx
Failures of weak approximation in families
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 7 / July 2016
- Published online by Cambridge University Press:
- 26 April 2016, pp. 1435-1475
- Print publication:
- July 2016
-
- Article
- Export citation
Dense clusters of primes in subsets
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 7 / July 2016
- Published online by Cambridge University Press:
- 01 April 2016, pp. 1517-1554
- Print publication:
- July 2016
-
- Article
-
- You have access
- Export citation
Minor arcs, mean values, and restriction theory for exponential sums over smooth numbers
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 6 / June 2016
- Published online by Cambridge University Press:
- 23 February 2016, pp. 1121-1158
- Print publication:
- June 2016
-
- Article
- Export citation
THE DIVISOR FUNCTION IN ARITHMETIC PROGRESSIONS MODULO PRIME POWERS
- Part of
-
- Journal:
- Mathematika / Volume 62 / Issue 3 / 2016
- Published online by Cambridge University Press:
- 17 May 2016, pp. 898-908
- Print publication:
- 2016
-
- Article
- Export citation
ON SUMS OF FOUR SQUARES OF PRIMES
- Part of
-
- Journal:
- Mathematika / Volume 62 / Issue 2 / 2016
- Published online by Cambridge University Press:
- 22 January 2016, pp. 348-361
- Print publication:
- 2016
-
- Article
- Export citation
BIG BIASES AMONGST PRODUCTS OF TWO PRIMES
- Part of
-
- Journal:
- Mathematika / Volume 62 / Issue 2 / 2016
- Published online by Cambridge University Press:
- 18 February 2016, pp. 502-507
- Print publication:
- 2016
-
- Article
- Export citation
PRIMES IN BEATTY SEQUENCES IN SHORT INTERVALS
- Part of
-
- Journal:
- Mathematika / Volume 62 / Issue 2 / 2016
- Published online by Cambridge University Press:
- 17 February 2016, pp. 572-586
- Print publication:
- 2016
-
- Article
- Export citation
On the sum of the square of a prime and a square-free number
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 19 / Issue 1 / 2016
- Published online by Cambridge University Press:
- 01 January 2016, pp. 16-24
-
- Article
-
- You have access
- Export citation
SIGN OF FOURIER COEFFICIENTS OF MODULAR FORMS OF HALF-INTEGRAL WEIGHT
- Part of
-
- Journal:
- Mathematika / Volume 62 / Issue 3 / 2016
- Published online by Cambridge University Press:
- 17 May 2016, pp. 866-883
- Print publication:
- 2016
-
- Article
- Export citation
STRONGLY
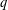 $q$-ADDITIVE FUNCTIONS AND DISTRIBUTIONAL PROPERTIES OF THE LARGEST PRIME FACTOR
$q$-ADDITIVE FUNCTIONS AND DISTRIBUTIONAL PROPERTIES OF THE LARGEST PRIME FACTOR
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 93 / Issue 2 / April 2016
- Published online by Cambridge University Press:
- 17 November 2015, pp. 177-185
- Print publication:
- April 2016
-
- Article
-
- You have access
- Export citation
REPRESENTATIONS OF INTEGERS BY THE BINARY QUADRATIC FORM
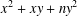 $x^{2}+xy+ny^{2}$
$x^{2}+xy+ny^{2}$
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 100 / Issue 2 / April 2016
- Published online by Cambridge University Press:
- 17 November 2015, pp. 182-191
- Print publication:
- April 2016
-
- Article
-
- You have access
- Export citation
ON THE SQUARE-FREE REPRESENTATION FUNCTION OF A NORM FORM AND NILSEQUENCES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 17 / Issue 1 / February 2018
- Published online by Cambridge University Press:
- 11 November 2015, pp. 107-135
- Print publication:
- February 2018
-
- Article
- Export citation
HELSON’S PROBLEM FOR SUMS OF A RANDOM MULTIPLICATIVE FUNCTION
- Part of
-
- Journal:
- Mathematika / Volume 62 / Issue 1 / 2016
- Published online by Cambridge University Press:
- 21 October 2015, pp. 101-110
- Print publication:
- 2016
-
- Article
- Export citation
ON THE NUMBER OF DIVISORS OF
 $n^{2}-1$
$n^{2}-1$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 93 / Issue 2 / April 2016
- Published online by Cambridge University Press:
- 02 October 2015, pp. 194-198
- Print publication:
- April 2016
-
- Article
-
- You have access
- Export citation
Heuristics on pairing-friendly abelian varieties
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 18 / Issue 1 / 2015
- Published online by Cambridge University Press:
- 01 June 2015, pp. 419-443
-
- Article
-
- You have access
- Export citation
THE JUMPING CHAMPION CONJECTURE
- Part of
-
- Journal:
- Mathematika / Volume 61 / Issue 3 / September 2015
- Published online by Cambridge University Press:
- 04 May 2015, pp. 719-740
- Print publication:
- September 2015
-
- Article
- Export citation
THE DISTRIBUTION OF 2-SELMER RANKS OF QUADRATIC TWISTS OF ELLIPTIC CURVES WITH PARTIAL TWO-TORSION
- Part of
-
- Journal:
- Mathematika / Volume 62 / Issue 1 / 2016
- Published online by Cambridge University Press:
- 04 May 2015, pp. 67-78
- Print publication:
- 2016
-
- Article
- Export citation
Théorèmes de type Fouvry–Iwaniec pour les entiers friables
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 5 / May 2015
- Published online by Cambridge University Press:
- 03 March 2015, pp. 828-862
- Print publication:
- May 2015
-
- Article
- Export citation
Squarefree values of trinomial discriminants
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 18 / Issue 1 / 2015
- Published online by Cambridge University Press:
- 01 January 2015, pp. 148-169
-
- Article
-
- You have access
- Export citation
ALMOST-PRIME VALUES OF BINARY FORMS WITH ONE PRIME VARIABLE
- Part of
-
- Journal:
- Mathematika / Volume 61 / Issue 3 / September 2015
- Published online by Cambridge University Press:
- 05 December 2014, pp. 741-755
- Print publication:
- September 2015
-
- Article
- Export citation