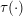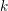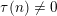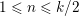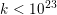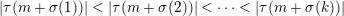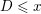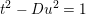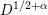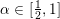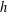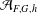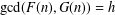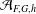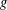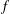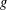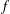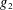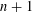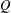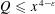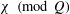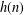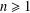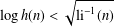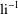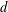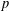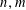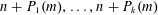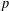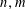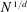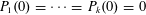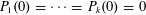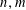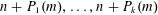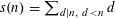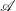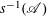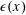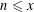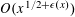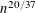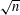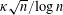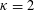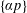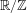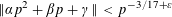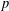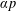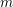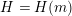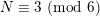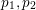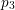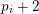Refine listing
Actions for selected content:
285 results in 11Nxx
Random ordering in modulus of consecutive Hecke eigenvalues of primitive forms
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 11 / November 2018
- Published online by Cambridge University Press:
- 18 October 2018, pp. 2441-2461
- Print publication:
- November 2018
-
- Article
- Export citation
Counting fundamental solutions to the Pell equation with prescribed size
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 11 / November 2018
- Published online by Cambridge University Press:
- 11 October 2018, pp. 2379-2402
- Print publication:
- November 2018
-
- Article
- Export citation
ON NUMBERS
 $n$ WITH POLYNOMIAL IMAGE COPRIME WITH THE
$n$ WITH POLYNOMIAL IMAGE COPRIME WITH THE  $n$TH TERM OF A LINEAR RECURRENCE
$n$TH TERM OF A LINEAR RECURRENCE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 99 / Issue 1 / February 2019
- Published online by Cambridge University Press:
- 28 August 2018, pp. 23-33
- Print publication:
- February 2019
-
- Article
-
- You have access
- Export citation
WHEN DOES THE BOMBIERI–VINOGRADOV THEOREM HOLD FOR A GIVEN MULTIPLICATIVE FUNCTION?
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 6 / 2018
- Published online by Cambridge University Press:
- 24 August 2018, e15
-
- Article
-
- You have access
- Open access
- Export citation
ON VALUES TAKEN BY THE LARGEST PRIME FACTOR OF SHIFTED PRIMES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 107 / Issue 1 / August 2019
- Published online by Cambridge University Press:
- 15 August 2018, pp. 133-144
- Print publication:
- August 2019
-
- Article
-
- You have access
- Export citation
ON BINARY CORRELATIONS OF MULTIPLICATIVE FUNCTIONS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 6 / 2018
- Published online by Cambridge University Press:
- 28 June 2018, e10
-
- Article
-
- You have access
- Open access
- Export citation
AN ARITHMETIC EQUIVALENCE OF THE RIEMANN HYPOTHESIS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 106 / Issue 2 / April 2019
- Published online by Cambridge University Press:
- 18 June 2018, pp. 235-273
- Print publication:
- April 2019
-
- Article
-
- You have access
- Export citation
IMPROVING AN INEQUALITY FOR THE DIVISOR FUNCTION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 97 / Issue 3 / June 2018
- Published online by Cambridge University Press:
- 28 March 2018, pp. 374-381
- Print publication:
- June 2018
-
- Article
-
- You have access
- Export citation
POLYNOMIAL PATTERNS IN THE PRIMES
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 6 / 2018
- Published online by Cambridge University Press:
- 12 February 2018, e1
-
- Article
-
- You have access
- Open access
- Export citation
LARGE BIAS FOR INTEGERS WITH PRIME FACTORS IN ARITHMETIC PROGRESSIONS
- Part of
-
- Journal:
- Mathematika / Volume 64 / Issue 1 / 2018
- Published online by Cambridge University Press:
- 15 February 2018, pp. 237-252
- Print publication:
- 2018
-
- Article
- Export citation
DIVISOR-SUM FIBERS
- Part of
-
- Journal:
- Mathematika / Volume 64 / Issue 2 / 2018
- Published online by Cambridge University Press:
- 03 April 2018, pp. 330-342
- Print publication:
- 2018
-
- Article
- Export citation
DENOMINATORS OF BERNOULLI POLYNOMIALS
- Part of
-
- Journal:
- Mathematika / Volume 64 / Issue 2 / 2018
- Published online by Cambridge University Press:
- 16 April 2018, pp. 519-541
- Print publication:
- 2018
-
- Article
- Export citation
THE PRIMES ARE NOT METRIC POISSONIAN
- Part of
-
- Journal:
- Mathematika / Volume 64 / Issue 1 / 2018
- Published online by Cambridge University Press:
- 14 February 2018, pp. 230-236
- Print publication:
- 2018
-
- Article
- Export citation
THE GOLDBACH PROBLEM FOR PRIMES THAT ARE SUMS OF TWO SQUARES PLUS ONE
- Part of
-
- Journal:
- Mathematika / Volume 64 / Issue 1 / 2018
- Published online by Cambridge University Press:
- 25 January 2018, pp. 20-70
- Print publication:
- 2018
-
- Article
- Export citation
TERNARY DIVISOR FUNCTIONS IN ARITHMETIC PROGRESSIONS TO SMOOTH MODULI
- Part of
-
- Journal:
- Mathematika / Volume 64 / Issue 3 / 2018
- Published online by Cambridge University Press:
- 19 June 2018, pp. 701-729
- Print publication:
- 2018
-
- Article
- Export citation
FRACTIONAL PARTS OF POLYNOMIALS OVER THE PRIMES. II
- Part of
-
- Journal:
- Mathematika / Volume 64 / Issue 3 / 2018
- Published online by Cambridge University Press:
- 26 June 2018, pp. 742-769
- Print publication:
- 2018
-
- Article
- Export citation
A note on multiplicative functions on progressions to large moduli
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 148 / Issue 1 / February 2018
- Published online by Cambridge University Press:
- 04 December 2017, pp. 63-77
- Print publication:
- February 2018
-
- Article
- Export citation
GENERALISED DIVISOR SUMS OF BINARY FORMS OVER NUMBER FIELDS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 1 / January 2020
- Published online by Cambridge University Press:
- 16 November 2017, pp. 137-173
- Print publication:
- January 2020
-
- Article
- Export citation
ON THE MINIMAL NUMBER OF SMALL ELEMENTS GENERATING FINITE PRIME FIELDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 96 / Issue 2 / October 2017
- Published online by Cambridge University Press:
- 17 August 2017, pp. 177-184
- Print publication:
- October 2017
-
- Article
-
- You have access
- Export citation
Vinogradov’s three primes theorem with almost twin primes
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 6 / June 2017
- Published online by Cambridge University Press:
- 20 April 2017, pp. 1220-1256
- Print publication:
- June 2017
-
- Article
- Export citation