Refine listing
Actions for selected content:
286 results in 11Nxx
On values taken by the largest prime factor of shifted primes
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 82 / Issue 1 / February 2007
- Published online by Cambridge University Press:
- 09 April 2009, pp. 133-147
- Print publication:
- February 2007
-
- Article
-
- You have access
- Export citation
The factorial moments of additive functions with rational argument
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 81 / Issue 3 / December 2006
- Published online by Cambridge University Press:
- 09 April 2009, pp. 425-440
- Print publication:
- December 2006
-
- Article
-
- You have access
- Export citation
An improvement of Artin's conjecture on average for composite moduli
- Part of
-
- Journal:
- Mathematika / Volume 51 / Issue 1-2 / December 2004
- Published online by Cambridge University Press:
- 26 February 2010, pp. 97-109
- Print publication:
- December 2004
-
- Article
- Export citation
On f(n) modulo Ω(n) and ω(n) when f is a polynomial
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 77 / Issue 2 / October 2004
- Published online by Cambridge University Press:
- 09 April 2009, pp. 149-164
- Print publication:
- October 2004
-
- Article
-
- You have access
- Export citation
The equation ω(n) = ω(n + 1)
- Part of
-
- Journal:
- Mathematika / Volume 50 / Issue 1-2 / December 2003
- Published online by Cambridge University Press:
- 26 February 2010, pp. 99-101
- Print publication:
- December 2003
-
- Article
- Export citation
Lattice points on circles
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 72 / Issue 2 / April 2002
- Published online by Cambridge University Press:
- 09 April 2009, pp. 217-222
- Print publication:
- April 2002
-
- Article
-
- You have access
- Export citation
Gaussian primes in narrow sectors
- Part of
-
- Journal:
- Mathematika / Volume 48 / Issue 1-2 / December 2001
- Published online by Cambridge University Press:
- 26 February 2010, pp. 119-135
- Print publication:
- December 2001
-
- Article
-
- You have access
- Export citation
Frequency of oscillations of an error term related to the Euler function
- Part of
-
- Journal:
- Mathematika / Volume 47 / Issue 1-2 / December 2000
- Published online by Cambridge University Press:
- 26 February 2010, pp. 161-164
- Print publication:
- December 2000
-
- Article
- Export citation
The order of inverses mod q
- Part of
-
- Journal:
- Mathematika / Volume 47 / Issue 1-2 / December 2000
- Published online by Cambridge University Press:
- 26 February 2010, pp. 87-108
- Print publication:
- December 2000
-
- Article
- Export citation
Sign changes of error terms related to the Euler function
- Part of
-
- Journal:
- Mathematika / Volume 46 / Issue 2 / December 1999
- Published online by Cambridge University Press:
- 26 February 2010, pp. 391-395
- Print publication:
- December 1999
-
- Article
- Export citation
On smooth gaps between consecutive prime numbers
- Part of
-
- Journal:
- Mathematika / Volume 46 / Issue 1 / June 1999
- Published online by Cambridge University Press:
- 26 February 2010, pp. 57-75
- Print publication:
- June 1999
-
- Article
- Export citation
Asymptotics of poisson approximation to random discrete distributions: an analytic approach
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 31 / Issue 2 / June 1999
- Published online by Cambridge University Press:
- 01 July 2016, pp. 448-491
- Print publication:
- June 1999
-
- Article
- Export citation
Piatetski-Shapiro prime k-tuplets
- Part of
-
- Journal:
- Mathematika / Volume 45 / Issue 2 / December 1998
- Published online by Cambridge University Press:
- 26 February 2010, pp. 351-357
- Print publication:
- December 1998
-
- Article
- Export citation
Hardy's legacy to number theory
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 65 / Issue 2 / October 1998
- Published online by Cambridge University Press:
- 09 April 2009, pp. 238-266
- Print publication:
- October 1998
-
- Article
-
- You have access
- Export citation
Uniform bounds for the least almost-prime primitive root
- Part of
-
- Journal:
- Mathematika / Volume 45 / Issue 1 / June 1998
- Published online by Cambridge University Press:
- 26 February 2010, pp. 191-207
- Print publication:
- June 1998
-
- Article
- Export citation
On strings of consecutive integers with no large prime factors
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 64 / Issue 2 / April 1998
- Published online by Cambridge University Press:
- 09 April 2009, pp. 266-276
- Print publication:
- April 1998
-
- Article
-
- You have access
- Export citation
Almost-prime k-tuples
- Part of
-
- Journal:
- Mathematika / Volume 44 / Issue 2 / December 1997
- Published online by Cambridge University Press:
- 26 February 2010, pp. 245-266
- Print publication:
- December 1997
-
- Article
- Export citation
On the eigenvalues of Redheffer's matrix, II
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 60 / Issue 2 / April 1996
- Published online by Cambridge University Press:
- 09 April 2009, pp. 260-273
- Print publication:
- April 1996
-
- Article
-
- You have access
- Export citation
A sharp inequality of Halász type for the mean value of a multiplicative arithmetic function
- Part of
-
- Journal:
- Mathematika / Volume 42 / Issue 1 / June 1995
- Published online by Cambridge University Press:
- 26 February 2010, pp. 144-157
- Print publication:
- June 1995
-
- Article
- Export citation
On recursive solutions of a unit fraction equation
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 57 / Issue 3 / December 1994
- Published online by Cambridge University Press:
- 09 April 2009, pp. 341-356
- Print publication:
- December 1994
-
- Article
-
- You have access
- Export citation
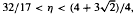 , there exists a constant
, there exists a constant 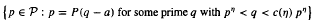 has relative asymptotic density one in the set of all prime numbers. Moreover, in the range
has relative asymptotic density one in the set of all prime numbers. Moreover, in the range 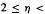
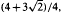 , one can take
, one can take 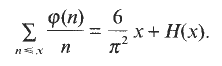
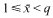 be such that
be such that 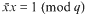 . For fixed
. For fixed 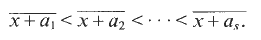
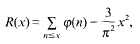
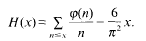
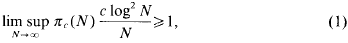
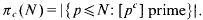
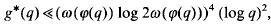
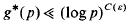
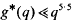 . However, there is not at present any stronger unconditional upper bound for
. However, there is not at present any stronger unconditional upper bound for 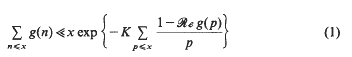
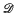 for all primes
for all primes 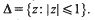 Thus our point of view is similar to that of Halász [Hz 2] in that we seek a general inequality in terms of simple quantities, albeit
Thus our point of view is similar to that of Halász [Hz 2] in that we seek a general inequality in terms of simple quantities, albeit 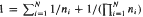 and discuss techniques for generating solutions. By examining a quadratic recurrence relation modulo a family of primes we have found some 500 new infinite sequences of solutions. We also initiate an investigation of the randomness of the distribution of solutions, and show that there are infinitely many solutions not generated by the aforementioned technique.
and discuss techniques for generating solutions. By examining a quadratic recurrence relation modulo a family of primes we have found some 500 new infinite sequences of solutions. We also initiate an investigation of the randomness of the distribution of solutions, and show that there are infinitely many solutions not generated by the aforementioned technique.