We consider the quadratic polynomial m2 + D and study the asymptotic formula for the number of integers m, 1≤ m ≤ M, for which the values of the polynomial are square-free. We are interested in particular in the question of how small we can take m in relation to D and still have the asymptotic hold.

Assuming a conjecture intermediate in strength between one of Chowla and one of Heath-Brown on the least prime in a residue class, we show that for any coprime integers a and m≥1, there are infinitely many Carmichael numbers in the arithmetic progression a mod m.

For each integer n ≥ 2, let β(n) stand for the product of the exponents in the prime factorization of n. Given an arbitrary integer k ≥ 2, let nk be the smallest positive integer n such that β(n + 1) = β(n + 2) = … = β(n + k). We prove that there exist positive constants c1 and c2 such that, for all integers k ≥ 2,

For a natural number n, let λ(n) denote the order of the largest cyclic subgroup of (ℤ/nℤ)*. For a given integer a, let Na(x) denote the number of n ≤ x coprime to a for which a has order λ(n) in (ℤ/nℤ)*. Let R(n) denote the number of elements of (ℤ/nℤ)* with order λ(n). It is natural to compare Na(x) with ∑n≤xR(n)/n. In this paper we show that the average of Na(x) for 1 ≤ a ≤ y is indeed asymptotic to this sum, provided y ≥ exp((2 + ε)(log x log log x)1/2), thus improving a theorem of the first author who had this for y ≥ exp((log x)3/4;). The result is to be compared with a similar theorem of Stephens who considered the case of prime numbers n.

Let R(n,θ) denote the number of representations of the natural number n as the sum of four squares, each composed only with primes not exceeding nθ/2. When θ>e−1/3 a lower bound for R(n,θ) of the expected order of magnitude is established, and when θ>365/592, it is shown that R(n,θ)>0 holds for large n. A similar result is obtained for sums of three squares. An asymptotic formula is obtained for the related problem of representing an integer as the sum of two squares and two squares composed of small primes, as above, for any fixed θ>0. This last result is the key to bound R(n,θ) from below.

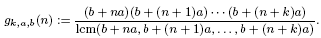
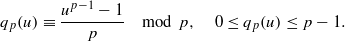
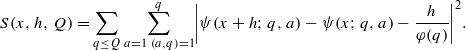
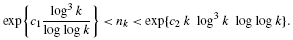
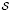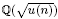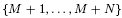Let u(n)=f(gn), where g > 1 is integer and f(X) ∈ ℤ[X] is non-constant and has no multiple roots. We use the theory of -unit equations as well as bounds for character sums to obtain a lower bound on the number of distinct fields among for n ∈ . Fields of this type include the Shanks fields and their generalizations.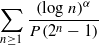

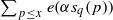Let P(k) be the largest prime factor of the positive integer k. In this paper, we prove that the series is convergent for each constant α<1/2, which gives a more precise form of a result of C. L. Stewart [‘On divisors of Fermat, Fibonacci, Lucas and Lehmer numbers’, Proc. London Math. Soc.35(3) (1977), 425–447].

Given an integer n≥2, let λ(n):=(log n)/(log γ(n)), where γ(n)=∏ p∣np, denote the index of composition of n, with λ(1)=1. Letting ϕ and σ stand for the Euler function and the sum of divisors function, we show that both λ(ϕ(n)) and λ(σ(n)) have normal order 1 and mean value 1. Given an arbitrary integer k≥2, we then study the size of min {λ(ϕ(n)),λ(ϕ(n+1)),…,λ(ϕ(n+k−1))} and of min {λ(σ(n)),λ(σ(n+1)),…,λ(σ(n+k−1))} as n becomes large.

The main goal of this paper is to provide asymptotic expansions for the numbers #{p≤x:p prime,sq(p)=k} for k close to ((q−1)/2)log qx, where sq(n) denotes the q-ary sum-of-digits function. The proof is based on a thorough analysis of exponential sums of the form (where the sum is restricted to p prime), for which we have to extend a recent result by the second two authors.

We revisit recent work of Heath-Brown on the average order of the quantity r(L1(x))⋯r(L4(x)), for suitable binary linear forms L1,…,L4, as x=(x1,x2) ranges over quite general regions in ℤ2. In addition to improving the error term in Heath-Brown’s estimate, we generalise his result to cover a wider class of linear forms.

We study a function field analog of Chebyshev’s bias. Our results, as well as their proofs, are similar to those of Rubinstein and Sarnak in the case of the rational number field. Following Rubinstein and Sarnak, we introduce the grand simplicity hypothesis (GSH), a certain hypothesis on the inverse zeros of Dirichlet L-series of a polynomial ring over a finite field. Under this hypothesis, we investigate how primes, that is, irreducible monic polynomials in a polynomial ring over a finite field, are distributed in a given set of residue classes modulo a fixed monic polynomial. In particular, we prove under the GSH that, like the number field case, primes are biased toward quadratic nonresidues. Unlike the number field case, the GSH can be proved to hold in some cases and can be violated in some other cases. Also, under the GSH, we give the necessary and sufficient conditions for which primes are unbiased and describe certain central limit behaviors as the degree of modulus under consideration tends to infinity, all of which have been established in the number field case by Rubinstein and Sarnak.

Following T. H. Chan, we consider the problem of approximation of a given rational fraction a/q by sums of several rational fractions a1/q1,…,an/qn with smaller denominators. We show that in the special cases of n=3 and n=4 and certain admissible ranges for the denominators q1,…,qn, one can improve a result of T. H. Chan by using a different approach.

We consider logarithmic averages, over friable integers, of non-negative multiplicative functions. Under logarithmic, one-sided or two-sided hypotheses, we obtain sharp estimates that improve upon known results in the literature regarding both the quality of the error term and the range of validity. The one-sided hypotheses correspond to classical sieve assumptions. They are applied to provide an effective form of the Johnsen–Selberg prime power sieve.

In this paper we study the size of the value set of the Carmichael λ-functions.

Let P denote the set of prime numbers, and let P(n) denote the largest prime factor of an integer n > 1. We show that, for every real number , there exists a constant c(η) > 1 such that for every integer a ≠ 0, the set has relative asymptotic density one in the set of all prime numbers. Moreover, in the range , one can take c(η) = 1+ε for any fixed ε > 0. In particular, our results imply that for every real number 0.486 ≤ b.thetav; ≤ 0.531, the relation P(q − a) ≍ qθ holds for infinitely many primes q. We use this result to derive a lower bound on the number of distinct prime divisor of the value of the Carmichael function taken on a product of shifted primes. Finally, we study iterates of the map q ↦ P(q - a) for a > 0, and show that for infinitely many primes q, this map can be iterated at least (log logq)1+o(1) times before it terminates.

We consider the weak convergence of the set of strongly additive functions f(q) with rational argument q. It is assumed that f(p) and f(1/p) ∈ {0, 1} for all primes. We obtain necessary and sufficient conditions of the convergence to the limit distribution. The proof is based on the method of factorial moments. Sieve results, and Halász's and Ruzsa's inequalities are used. We present a few examples of application of the given results to some sets of fractions.

Let q be a natural number. When the multiplicative iroup (ℤ/qℤ)* is a cyclic group, its generators are called primitive roots. Note that the generators are also elements with the maximum order if (ℤ/qℤ)* is cyclic. Thus, when (ℤ–qℤ)* is not a cyclic goup, we then call an element with: he maximal possible order a primitive root, which was initially introduced by R. Carmichael [1].

In this paper we show that if f (X) ∈; Z [X ] is a nonzero polynomial, then ω(n)/f(n) holds only on a set of n of asymptotic density zero, where for a positive integer n the number ω(n) counts the number of distinct prime factors ofn.

It is proved that there are infinitely many integers n such that n and n + 1 have the same number of distinct prime divisors.

We prove that the lattice points on the circles x2 + y2 = n are well distributed for most circles containing lattice points.