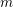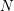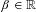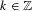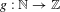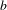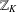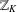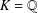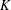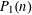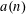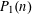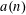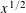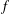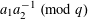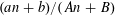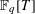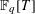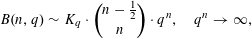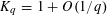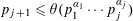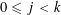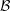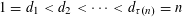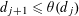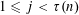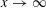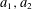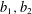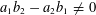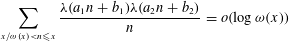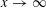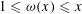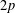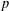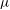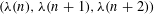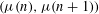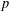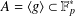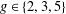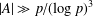Refine listing
Actions for selected content:
286 results in 11Nxx
Vinogradov’s three primes theorem with almost twin primes
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 6 / June 2017
- Published online by Cambridge University Press:
- 20 April 2017, pp. 1220-1256
- Print publication:
- June 2017
-
- Article
- Export citation
PROPRIÉTÉS LOCALES DES CHIFFRES DES NOMBRES PREMIERS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 18 / Issue 1 / January 2019
- Published online by Cambridge University Press:
- 04 April 2017, pp. 189-224
- Print publication:
- January 2019
-
- Article
- Export citation
TWO PROBLEMS CONCERNING IRREDUCIBLE ELEMENTS IN RINGS OF INTEGERS OF NUMBER FIELDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 96 / Issue 1 / August 2017
- Published online by Cambridge University Press:
- 02 March 2017, pp. 44-58
- Print publication:
- August 2017
-
- Article
-
- You have access
- Export citation
Une nouvelle approche dans la théorie des entiers friables
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 3 / March 2017
- Published online by Cambridge University Press:
- 20 February 2017, pp. 453-473
- Print publication:
- March 2017
-
- Article
- Export citation
FRACTIONAL PARTS OF POLYNOMIALS OVER THE PRIMES
- Part of
-
- Journal:
- Mathematika / Volume 63 / Issue 3 / 2017
- Published online by Cambridge University Press:
- 29 November 2017, pp. 715-733
- Print publication:
- 2017
-
- Article
- Export citation
RANDOM MULTIPLICATIVE WALKS ON THE RESIDUES MODULO
 $n$
$n$
- Part of
-
- Journal:
- Mathematika / Volume 63 / Issue 2 / 2017
- Published online by Cambridge University Press:
- 12 May 2017, pp. 602-621
- Print publication:
- 2017
-
- Article
- Export citation
PRIMES AND PRIME IDEALS IN SHORT INTERVALS
- Part of
-
- Journal:
- Mathematika / Volume 63 / Issue 2 / 2017
- Published online by Cambridge University Press:
- 09 February 2017, pp. 364-371
- Print publication:
- 2017
-
- Article
-
- You have access
- HTML
- Export citation
SMOOTH-SUPPORTED MULTIPLICATIVE FUNCTIONS IN ARITHMETIC PROGRESSIONS BEYOND THE
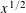 $x^{1/2}$ -BARRIER
$x^{1/2}$ -BARRIER
- Part of
-
- Journal:
- Mathematika / Volume 63 / Issue 3 / 2017
- Published online by Cambridge University Press:
- 29 November 2017, pp. 895-918
- Print publication:
- 2017
-
- Article
- Export citation
ON THE LEAST SQUAREFREE NUMBER INAN ARITHMETIC PROGRESSION
- Part of
-
- Journal:
- Mathematika / Volume 63 / Issue 2 / 2017
- Published online by Cambridge University Press:
- 23 March 2017, pp. 483-498
- Print publication:
- 2017
-
- Article
- Export citation
ON MULTIPLICATIVE COMPOSITIONS OF INTEGERS
- Part of
-
- Journal:
- Mathematika / Volume 63 / Issue 3 / 2017
- Published online by Cambridge University Press:
- 29 November 2017, pp. 1081-1090
- Print publication:
- 2017
-
- Article
- Export citation
PRIME NUMBER THEOREM EQUIVALENCES AND NON-EQUIVALENCES
- Part of
-
- Journal:
- Mathematika / Volume 63 / Issue 3 / 2017
- Published online by Cambridge University Press:
- 29 November 2017, pp. 852-862
- Print publication:
- 2017
-
- Article
- Export citation
HARMONIC ANALYSIS ON THE POSITIVE RATIONALS. DETERMINATION OF THE GROUP GENERATED BY THE RATIOS
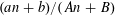 $(an+b)/(An+B)$
$(an+b)/(An+B)$
- Part of
-
- Journal:
- Mathematika / Volume 63 / Issue 3 / 2017
- Published online by Cambridge University Press:
- 29 November 2017, pp. 919-943
- Print publication:
- 2017
-
- Article
- Export citation
A POLYNOMIAL ANALOGUE OF LANDAU’S THEOREM AND RELATED PROBLEMS
- Part of
-
- Journal:
- Mathematika / Volume 63 / Issue 2 / 2017
- Published online by Cambridge University Press:
- 05 June 2017, pp. 622-665
- Print publication:
- 2017
-
- Article
- Export citation
ON A NEW CIRCLE PROBLEM
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 103 / Issue 2 / October 2017
- Published online by Cambridge University Press:
- 08 November 2016, pp. 231-249
- Print publication:
- October 2017
-
- Article
-
- You have access
- Export citation
A SIEVE PROBLEM AND ITS APPLICATION
- Part of
-
- Journal:
- Mathematika / Volume 63 / Issue 1 / 2017
- Published online by Cambridge University Press:
- 27 September 2016, pp. 213-229
- Print publication:
- 2017
-
- Article
- Export citation
THE LOGARITHMICALLY AVERAGED CHOWLA AND ELLIOTT CONJECTURES FOR TWO-POINT CORRELATIONS
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 4 / 2016
- Published online by Cambridge University Press:
- 27 September 2016, e8
-
- Article
-
- You have access
- Open access
- Export citation
RAMANUJAN CAYLEY GRAPHS OF FROBENIUS GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 94 / Issue 3 / December 2016
- Published online by Cambridge University Press:
- 26 September 2016, pp. 373-383
- Print publication:
- December 2016
-
- Article
-
- You have access
- Export citation
Sur les processus arithmétiques liés aux diviseurs
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 48 / Issue A / July 2016
- Published online by Cambridge University Press:
- 25 July 2016, pp. 63-76
- Print publication:
- July 2016
-
- Article
- Export citation
SIGN PATTERNS OF THE LIOUVILLE AND MÖBIUS FUNCTIONS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 4 / 2016
- Published online by Cambridge University Press:
- 21 June 2016, e14
-
- Article
-
- You have access
- Open access
- Export citation
ALMOST ALL PRIMES HAVE A MULTIPLE OF SMALL HAMMING WEIGHT
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 94 / Issue 2 / October 2016
- Published online by Cambridge University Press:
- 23 May 2016, pp. 224-235
- Print publication:
- October 2016
-
- Article
-
- You have access
- Export citation