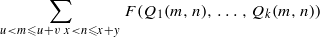Refine listing
Actions for selected content:
286 results in 11Nxx
Lifting, restricting and sifting integral points on affine homogeneous varieties
- Part of
-
- Journal:
- Compositio Mathematica / Volume 148 / Issue 6 / November 2012
- Published online by Cambridge University Press:
- 11 October 2012, pp. 1695-1716
- Print publication:
- November 2012
-
- Article
-
- You have access
- Export citation
A NOTE ON THE DISTRIBUTION FUNCTION OF
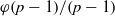 $ \varphi (\lowercase {P}-1)/(\lowercase {P}-1)$
$ \varphi (\lowercase {P}-1)/(\lowercase {P}-1)$
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 93 / Issue 1-2 / October 2012
- Published online by Cambridge University Press:
- 16 January 2013, pp. 77-83
- Print publication:
- October 2012
-
- Article
-
- You have access
- Export citation
WEAK PROPER DISTRIBUTION OF VALUES OF MULTIPLICATIVE FUNCTIONS IN RESIDUE CLASSES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 93 / Issue 1-2 / October 2012
- Published online by Cambridge University Press:
- 04 February 2013, pp. 173-188
- Print publication:
- October 2012
-
- Article
-
- You have access
- Export citation
BETWEEN THE PROBLEMS OF PÓLYA AND TURÁN
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 93 / Issue 1-2 / October 2012
- Published online by Cambridge University Press:
- 27 September 2012, pp. 157-171
- Print publication:
- October 2012
-
- Article
-
- You have access
- Export citation
ON THE RANKIN–SELBERG ZETA FUNCTION
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 93 / Issue 1-2 / October 2012
- Published online by Cambridge University Press:
- 19 September 2012, pp. 101-113
- Print publication:
- October 2012
-
- Article
-
- You have access
- Export citation
THE RESONANCE METHOD FOR LARGE CHARACTER SUMS
- Part of
-
- Journal:
- Mathematika / Volume 59 / Issue 1 / January 2013
- Published online by Cambridge University Press:
- 11 September 2012, pp. 87-118
- Print publication:
- January 2013
-
- Article
- Export citation
THE MONTGOMERY–HOOLEY THEOREM IN SHORT INTERVALS
- Part of
-
- Journal:
- Mathematika / Volume 59 / Issue 1 / January 2013
- Published online by Cambridge University Press:
- 02 August 2012, pp. 129-139
- Print publication:
- January 2013
-
- Article
- Export citation
Averages of shifted convolutions of d3(n)
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 55 / Issue 3 / October 2012
- Published online by Cambridge University Press:
- 12 April 2012, pp. 551-576
-
- Article
-
- You have access
- Export citation
ON SELMER GROUPS AND TATE–SHAFAREVICH GROUPS FOR ELLIPTIC CURVES y2=x3−n3
- Part of
-
- Journal:
- Mathematika / Volume 58 / Issue 2 / July 2012
- Published online by Cambridge University Press:
- 12 April 2012, pp. 236-274
- Print publication:
- July 2012
-
- Article
- Export citation
COUNTING FIXED POINTS, TWO-CYCLES, AND COLLISIONS OF THE DISCRETE EXPONENTIAL FUNCTION USING p-ADIC METHODS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 92 / Issue 2 / April 2012
- Published online by Cambridge University Press:
- 22 November 2012, pp. 163-178
- Print publication:
- April 2012
-
- Article
-
- You have access
- Export citation
PRODUCTS OF SHIFTED PRIMES SIMULTANEOUSLY TAKING PERFECT POWER VALUES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 92 / Issue 2 / April 2012
- Published online by Cambridge University Press:
- 19 September 2012, pp. 145-154
- Print publication:
- April 2012
-
- Article
-
- You have access
- Export citation
Products of three pairwise coprime integers in short intervals
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 15 / May 2012
- Published online by Cambridge University Press:
- 01 April 2012, pp. 59-70
-
- Article
-
- You have access
- Export citation
ON THE EQUATION f(g(x))=f(x)hm(x) FOR COMPOSITE POLYNOMIALS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 92 / Issue 2 / April 2012
- Published online by Cambridge University Press:
- 19 September 2012, pp. 155-161
- Print publication:
- April 2012
-
- Article
-
- You have access
- Export citation
On numbers n dividing the nth term of a linear recurrence
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 55 / Issue 2 / June 2012
- Published online by Cambridge University Press:
- 23 February 2012, pp. 271-289
-
- Article
-
- You have access
- Export citation
ON A CONJECTURE OF ERDŐS
- Part of
-
- Journal:
- Mathematika / Volume 58 / Issue 2 / July 2012
- Published online by Cambridge University Press:
- 23 February 2012, pp. 275-289
- Print publication:
- July 2012
-
- Article
- Export citation
ON THE DISTRIBUTION OF TORSION POINTS MODULO PRIMES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 86 / Issue 2 / October 2012
- Published online by Cambridge University Press:
- 16 February 2012, pp. 339-347
- Print publication:
- October 2012
-
- Article
-
- You have access
- Export citation
INFINITUDE OF ELLIPTIC CARMICHAEL NUMBERS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 92 / Issue 1 / February 2012
- Published online by Cambridge University Press:
- 25 April 2012, pp. 45-60
- Print publication:
- February 2012
-
- Article
-
- You have access
- Export citation
MOYENNES DE FONCTIONS ARITHMÉTIQUES DE FORMES BINAIRES
- Part of
-
- Journal:
- Mathematika / Volume 58 / Issue 2 / July 2012
- Published online by Cambridge University Press:
- 19 January 2012, pp. 290-304
- Print publication:
- July 2012
-
- Article
- Export citation
POWER-FREE VALUES OF THE POLYNOMIAL t1⋯tr−1
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 85 / Issue 1 / February 2012
- Published online by Cambridge University Press:
- 23 September 2011, pp. 154-163
- Print publication:
- February 2012
-
- Article
-
- You have access
- Export citation
ON A PROBLEM ON NORMAL NUMBERS RAISED BY IGOR SHPARLINSKI
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 84 / Issue 2 / October 2011
- Published online by Cambridge University Press:
- 16 June 2011, pp. 337-349
- Print publication:
- October 2011
-
- Article
-
- You have access
- Export citation
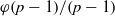
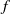
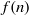
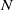
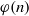
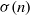
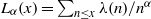
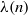

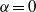
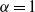
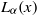
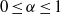
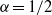
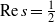
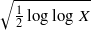 as
as 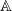 be a commutative algebraic group defined over a number field
be a commutative algebraic group defined over a number field 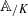 , we determine the average values of
, we determine the average values of