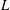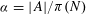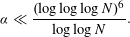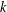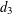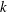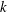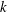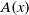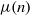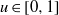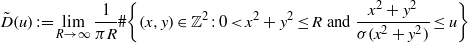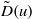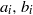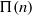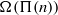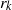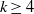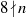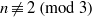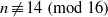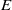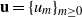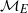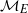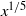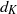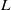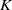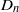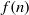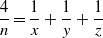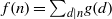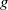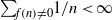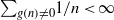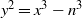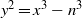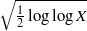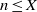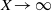Refine listing
Actions for selected content:
286 results in 11Nxx
AN
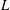 $L$ -FUNCTION-FREE PROOF OF VINOGRADOV’S THREE PRIMES THEOREM
$L$ -FUNCTION-FREE PROOF OF VINOGRADOV’S THREE PRIMES THEOREM
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 2 / 01 July 2014
- Published online by Cambridge University Press:
- 04 November 2014, e27
-
- Article
-
- You have access
- Open access
- Export citation
ON IMPROVING ROTH’S THEOREM IN THE PRIMES
- Part of
-
- Journal:
- Mathematika / Volume 61 / Issue 1 / January 2015
- Published online by Cambridge University Press:
- 09 October 2014, pp. 49-62
- Print publication:
- January 2015
-
- Article
- Export citation
THE DISTRIBUTION OF
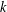 $k$ -TUPLES OF REDUCED RESIDUES
$k$ -TUPLES OF REDUCED RESIDUES
- Part of
-
- Journal:
- Mathematika / Volume 61 / Issue 1 / January 2015
- Published online by Cambridge University Press:
- 13 August 2014, pp. 72-88
- Print publication:
- January 2015
-
- Article
- Export citation
Corrigendum: Elliptic curves with a given number of points over finite fields
- Part of
-
- Journal:
- Compositio Mathematica / Volume 150 / Issue 8 / August 2014
- Published online by Cambridge University Press:
- 17 July 2014, pp. 1347-1348
- Print publication:
- August 2014
-
- Article
-
- You have access
- Export citation
ON THE EXPONENT OF DISTRIBUTION OF THE TERNARY DIVISOR FUNCTION
- Part of
-
- Journal:
- Mathematika / Volume 61 / Issue 1 / January 2015
- Published online by Cambridge University Press:
- 02 June 2014, pp. 121-144
- Print publication:
- January 2015
-
- Article
- Export citation
THE MINIMAL GROWTH OF A
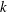 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}k$-REGULAR SEQUENCE
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}k$-REGULAR SEQUENCE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 90 / Issue 2 / October 2014
- Published online by Cambridge University Press:
- 22 May 2014, pp. 195-203
- Print publication:
- October 2014
-
- Article
-
- You have access
- Export citation
Strong orthogonality between the Möbius function, additive characters and Fourier coefficients of cusp forms
- Part of
-
- Journal:
- Compositio Mathematica / Volume 150 / Issue 5 / May 2014
- Published online by Cambridge University Press:
- 24 April 2014, pp. 763-797
- Print publication:
- May 2014
-
- Article
- Export citation
THE ERROR TERM IN THE COUNT OF ABUNDANT NUMBERS
- Part of
-
- Journal:
- Mathematika / Volume 60 / Issue 1 / January 2014
- Published online by Cambridge University Press:
- 02 January 2014, pp. 43-65
- Print publication:
- January 2014
-
- Article
- Export citation
VARIATIONS ON A THEOREM OF DAVENPORT CONCERNING ABUNDANT NUMBERS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 89 / Issue 3 / June 2014
- Published online by Cambridge University Press:
- 12 September 2013, pp. 437-450
- Print publication:
- June 2014
-
- Article
-
- You have access
- Export citation
ALMOST-PRIME
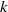 $k$-TUPLES
$k$-TUPLES
- Part of
-
- Journal:
- Mathematika / Volume 60 / Issue 1 / January 2014
- Published online by Cambridge University Press:
- 06 September 2013, pp. 108-138
- Print publication:
- January 2014
-
- Article
- Export citation
Knots which behave like the prime numbers
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 8 / August 2013
- Published online by Cambridge University Press:
- 10 July 2013, pp. 1235-1244
- Print publication:
- August 2013
-
- Article
- Export citation
ON WARING’S PROBLEM: TWO SQUARES AND THREE BIQUADRATES
- Part of
-
- Journal:
- Mathematika / Volume 60 / Issue 1 / January 2014
- Published online by Cambridge University Press:
- 28 June 2013, pp. 153-165
- Print publication:
- January 2014
-
- Article
- Export citation
Pretentious multiplicative functions and the prime number theorem for arithmetic progressions
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 7 / July 2013
- Published online by Cambridge University Press:
- 14 May 2013, pp. 1129-1149
- Print publication:
- July 2013
-
- Article
- Export citation
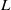 $L$-FUNCTIONS OF ELLIPTIC CURVES AND BINARY RECURRENCES
$L$-FUNCTIONS OF ELLIPTIC CURVES AND BINARY RECURRENCES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 88 / Issue 3 / December 2013
- Published online by Cambridge University Press:
- 22 March 2013, pp. 509-519
- Print publication:
- December 2013
-
- Article
-
- You have access
- Export citation
CARMICHAEL NUMBERS IN ARITHMETIC PROGRESSIONS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 94 / Issue 2 / April 2013
- Published online by Cambridge University Press:
- 08 March 2013, pp. 268-275
- Print publication:
- April 2013
-
- Article
-
- You have access
- Export citation
Logarithmic derivatives of Artin
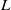 $L$-functions
$L$-functions
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 4 / April 2013
- Published online by Cambridge University Press:
- 26 February 2013, pp. 568-586
- Print publication:
- April 2013
-
- Article
- Export citation
COUNTING THE NUMBER OF SOLUTIONS TO THE ERDŐS–STRAUS EQUATION ON UNIT FRACTIONS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 94 / Issue 1 / February 2013
- Published online by Cambridge University Press:
- 15 May 2013, pp. 50-105
- Print publication:
- February 2013
-
- Article
-
- You have access
- Export citation
UNCERTAINTY PRINCIPLES CONNECTED WITH THE MÖBIUS INVERSION FORMULA
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 88 / Issue 3 / December 2013
- Published online by Cambridge University Press:
- 25 January 2013, pp. 460-472
- Print publication:
- December 2013
-
- Article
-
- You have access
- Export citation
ON SELMER GROUPS OF QUADRATIC TWISTS OF ELLIPTIC CURVES WITH A TWO-TORSION OVER
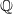 $\mathbb {Q}$
$\mathbb {Q}$
- Part of
-
- Journal:
- Mathematika / Volume 59 / Issue 2 / July 2013
- Published online by Cambridge University Press:
- 15 January 2013, pp. 303-319
- Print publication:
- July 2013
-
- Article
- Export citation
Elliptic curves with a given number of points over finite fields
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 2 / February 2013
- Published online by Cambridge University Press:
- 01 November 2012, pp. 175-203
- Print publication:
- February 2013
-
- Article
- Export citation