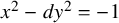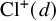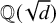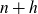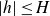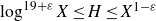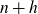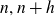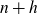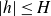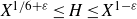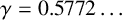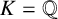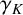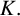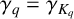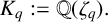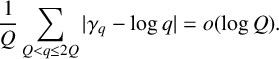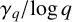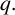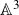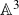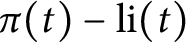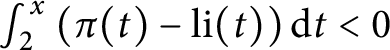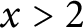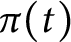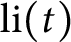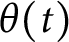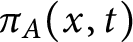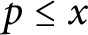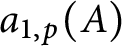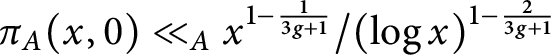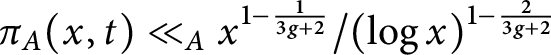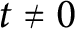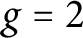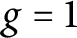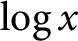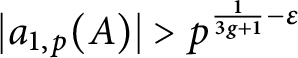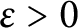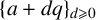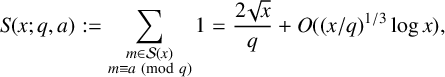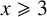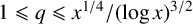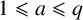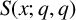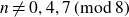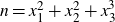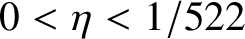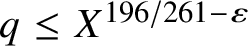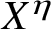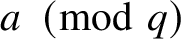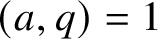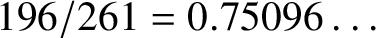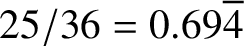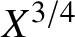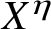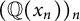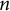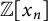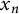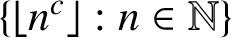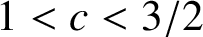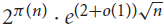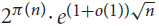Refine listing
Actions for selected content:
285 results in 11Nxx
The 8-rank of the narrow class group and the negative Pell equation
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 21 June 2022, e46
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Correlations of almost primes
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 174 / Issue 2 / March 2023
- Published online by Cambridge University Press:
- 09 June 2022, pp. 301-344
- Print publication:
- March 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
EULER–KRONECKER CONSTANTS FOR CYCLOTOMIC FIELDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 107 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 30 May 2022, pp. 79-84
- Print publication:
- February 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Higher rank motivic Donaldson–Thomas invariants of
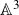 $\mathbb A^3$ via wall-crossing, and asymptotics
$\mathbb A^3$ via wall-crossing, and asymptotics
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 174 / Issue 1 / January 2023
- Published online by Cambridge University Press:
- 05 May 2022, pp. 97-122
- Print publication:
- January 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the average value of
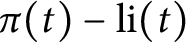 $\pi (t)-\operatorname {\textrm {li}}(t)$
$\pi (t)-\operatorname {\textrm {li}}(t)$
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 14 March 2022, pp. 185-195
- Print publication:
- March 2023
-
- Article
- Export citation
Bounds for the distribution of the Frobenius traces associated to products of non-CM elliptic curves
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 3 / June 2023
- Published online by Cambridge University Press:
- 07 March 2022, pp. 687-712
- Print publication:
- June 2023
-
- Article
- Export citation
DISTRIBUTION OF ELEMENTS OF A FLOOR FUNCTION SET IN ARITHMETICAL PROGRESSIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 3 / December 2022
- Published online by Cambridge University Press:
- 01 March 2022, pp. 419-424
- Print publication:
- December 2022
-
- Article
- Export citation
Uniform bounds for norms of theta series and arithmetic applications
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 173 / Issue 3 / November 2022
- Published online by Cambridge University Press:
- 28 February 2022, pp. 669-691
- Print publication:
- November 2022
-
- Article
- Export citation
AN EXPLICIT VERSION OF CHEN’S THEOREM
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 2 / April 2022
- Published online by Cambridge University Press:
- 08 February 2022, pp. 344-346
- Print publication:
- April 2022
-
- Article
-
- You have access
- HTML
- Export citation
A GENERALISATION OF A THEOREM OF ERDŐS AND NIVEN
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 2 / October 2022
- Published online by Cambridge University Press:
- 24 January 2022, pp. 215-223
- Print publication:
- October 2022
-
- Article
- Export citation
ON QUOTIENTS OF VALUES OF EULER’S FUNCTION ON FACTORIALS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 3 / June 2022
- Published online by Cambridge University Press:
- 17 November 2021, pp. 353-364
- Print publication:
- June 2022
-
- Article
- Export citation
Squarefree Integers in Arithmetic Progressions to Smooth Moduli
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 27 October 2021, e72
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A dynamical characterization for monogenity at every level of some infinite
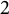 $2$-towers
$2$-towers
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 20 October 2021, pp. 806-814
- Print publication:
- September 2022
-
- Article
- Export citation
CONSECUTIVE SQUARE-FREE NUMBERS IN PIATETSKI-SHAPIRO SEQUENCES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 2 / April 2022
- Published online by Cambridge University Press:
- 13 September 2021, pp. 217-222
- Print publication:
- April 2022
-
- Article
- Export citation
Counting and equidistribution in quaternionic Heisenberg groups
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 173 / Issue 1 / July 2022
- Published online by Cambridge University Press:
- 08 July 2021, pp. 67-104
- Print publication:
- July 2022
-
- Article
- Export citation
Joint Poisson distribution of prime factors in sets
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 173 / Issue 1 / July 2022
- Published online by Cambridge University Press:
- 23 June 2021, pp. 189-200
- Print publication:
- July 2022
-
- Article
- Export citation
Most permutations power to a cycle of small prime length
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 64 / Issue 2 / May 2021
- Published online by Cambridge University Press:
- 24 May 2021, pp. 234-246
-
- Article
- Export citation
Cyclicity of elliptic curves modulo primes in arithmetic progressions
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 74 / Issue 5 / October 2022
- Published online by Cambridge University Press:
- 03 May 2021, pp. 1277-1309
- Print publication:
- October 2022
-
- Article
- Export citation
Prime number theorem for regular Toeplitz subshifts
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 4 / April 2022
- Published online by Cambridge University Press:
- 15 February 2021, pp. 1446-1473
- Print publication:
- April 2022
-
- Article
- Export citation
The number of maximum primitive sets of integers
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 30 / Issue 5 / September 2021
- Published online by Cambridge University Press:
- 28 January 2021, pp. 781-795
-
- Article
- Export citation