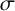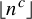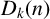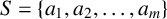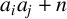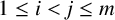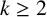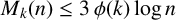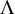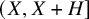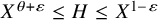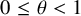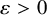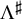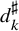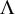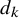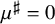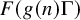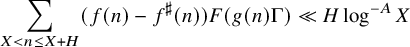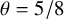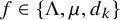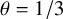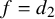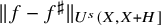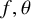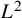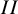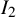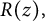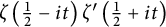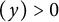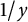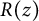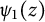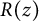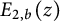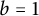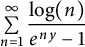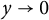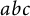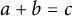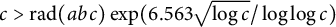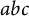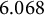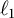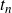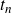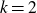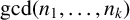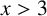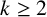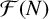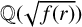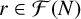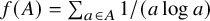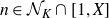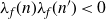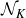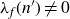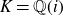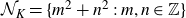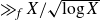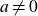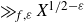Refine listing
Actions for selected content:
285 results in 11Nxx
ENERGY BOUNDS FOR MODULAR ROOTS AND THEIR APPLICATIONS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 5 / September 2025
- Published online by Cambridge University Press:
- 04 March 2024, pp. 1765-1806
- Print publication:
- September 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Joint partial equidistribution of Farey rays in negatively curved manifolds and trees
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 9 / September 2024
- Published online by Cambridge University Press:
- 08 January 2024, pp. 2700-2736
- Print publication:
- September 2024
-
- Article
- Export citation
A NOTE ON THE ZEROS OF L-FUNCTIONS ASSOCIATED TO FIXED-ORDER DIRICHLET CHARACTERS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 110 / Issue 2 / October 2024
- Published online by Cambridge University Press:
- 18 December 2023, pp. 252-261
- Print publication:
- October 2024
-
- Article
- Export citation
Bracket words along Hardy field sequences
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 9 / September 2024
- Published online by Cambridge University Press:
- 14 December 2023, pp. 2621-2648
- Print publication:
- September 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
NEW EFFECTIVE RESULTS IN THE THEORY OF THE RIEMANN ZETA-FUNCTION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 12 December 2023, pp. 403-406
- Print publication:
- April 2024
-
- Article
-
- You have access
- HTML
- Export citation
HIGHER MOMENT FORMULAE AND LIMITING DISTRIBUTIONS OF LATTICE POINTS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 5 / September 2024
- Published online by Cambridge University Press:
- 28 November 2023, pp. 2081-2125
- Print publication:
- September 2024
-
- Article
- Export citation
Generalized divisor functions in arithmetic progressions: II
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 16 November 2023, pp. 28-56
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
AN EFFECTIVE BOUND FOR GENERALISED DIOPHANTINE m-TUPLES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 06 November 2023, pp. 242-253
- Print publication:
- April 2024
-
- Article
- Export citation
Smooth integers and de Bruijn's approximation Ʌ
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 155 / Issue 3 / June 2025
- Published online by Cambridge University Press:
- 31 October 2023, pp. 792-820
- Print publication:
- June 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Higher uniformity of arithmetic functions in short intervals I. All intervals
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 11 / 2023
- Published online by Cambridge University Press:
- 19 October 2023, e29
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Lambert series of logarithm, the derivative of Deninger’s function
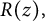 $R(z),$ and a mean value theorem for
$R(z),$ and a mean value theorem for 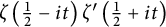 $\zeta \left (\frac {1}{2}-it\right )\zeta '\left (\frac {1}{2}+it\right )$
$\zeta \left (\frac {1}{2}-it\right )\zeta '\left (\frac {1}{2}+it\right )$
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 5 / October 2024
- Published online by Cambridge University Press:
- 11 October 2023, pp. 1695-1730
- Print publication:
- October 2024
-
- Article
- Export citation
A new lower bound in the
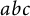 $abc$ conjecture
$abc$ conjecture
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 09 October 2023, pp. 369-378
- Print publication:
- June 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A problem of Erdős–Graham–Granville–Selfridge on integral points on hyperelliptic curves
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 176 / Issue 2 / March 2024
- Published online by Cambridge University Press:
- 05 October 2023, pp. 309-323
- Print publication:
- March 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Dirichlet law for factorisation of integers, polynomials and permutations
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 175 / Issue 3 / November 2023
- Published online by Cambridge University Press:
- 06 September 2023, pp. 649-676
- Print publication:
- November 2023
-
- Article
- Export citation
ON SUMS INVOLVING THE EULER TOTIENT FUNCTION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 3 / June 2024
- Published online by Cambridge University Press:
- 24 August 2023, pp. 486-497
- Print publication:
- June 2024
-
- Article
- Export citation
ON QUADRATIC FIELDS GENERATED BY POLYNOMIALS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 3 / June 2024
- Published online by Cambridge University Press:
- 29 June 2023, pp. 476-485
- Print publication:
- June 2024
-
- Article
- Export citation
EXPLICIT ESTIMATES FOR THE DISTRIBUTION OF PRIMES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 2 / October 2023
- Published online by Cambridge University Press:
- 22 June 2023, pp. 341-342
- Print publication:
- October 2023
-
- Article
-
- You have access
- HTML
- Export citation
Smooth numbers with few nonzero binary digits
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 20 June 2023, pp. 74-89
- Print publication:
- March 2024
-
- Article
- Export citation
A proof of the Erdős primitive set conjecture
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 11 / 2023
- Published online by Cambridge University Press:
- 14 June 2023, e18
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Sign changes of fourier coefficients of holomorphic cusp forms at norm form arguments
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 175 / Issue 3 / November 2023
- Published online by Cambridge University Press:
- 23 May 2023, pp. 539-567
- Print publication:
- November 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation