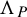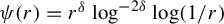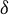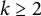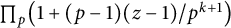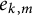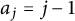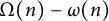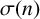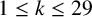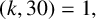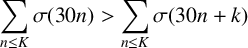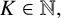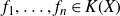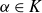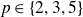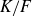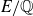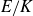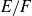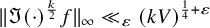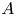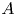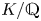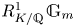Refine listing
Actions for selected content:
285 results in 11Nxx
On Gaussian primes in sparse sets
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 2 / February 2025
- Published online by Cambridge University Press:
- 17 June 2025, pp. 181-243
- Print publication:
- February 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A function field analog of Jacobi’s theorem on sums of squares and its moments
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 10 January 2025, pp. 667-683
- Print publication:
- September 2025
-
- Article
- Export citation
A NOTE ON THE LARGE SIEVE INEQUALITY FOR MODULI GENERATED BY A QUADRATIC
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 112 / Issue 2 / October 2025
- Published online by Cambridge University Press:
- 26 December 2024, pp. 254-259
- Print publication:
- October 2025
-
- Article
- Export citation
Bilinear Kloosterman sums in function fields and the distribution of irreducible polynomials
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 20 December 2024, pp. 1-26
-
- Article
- Export citation
THE DISTRIBUTION OF PRIME NUMBERS IN SHORT INTERVALS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 111 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 25 November 2024, pp. 174-176
- Print publication:
- February 2025
-
- Article
-
- You have access
- HTML
- Export citation
Product of polynomial values being large power
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 68 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 18 November 2024, pp. 51-62
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Convolution of periodic multiplicative functions and the divisor problem
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 77 / Issue 6 / December 2025
- Published online by Cambridge University Press:
- 14 November 2024, pp. 1966-1984
- Print publication:
- December 2025
-
- Article
- Export citation
Exact dimension functions of the prime continued fraction Cantor set
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 6 / June 2025
- Published online by Cambridge University Press:
- 14 November 2024, pp. 1757-1776
- Print publication:
- June 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Distribution of the number of prime factors with a given multiplicity
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 07 November 2024, pp. 1107-1122
- Print publication:
- December 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The Brun–Hooley sieve for 𝔽2[X] and squarefree shifts of integer polynomials
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 4 / November 2024
- Published online by Cambridge University Press:
- 06 November 2024, pp. 1171-1195
-
- Article
- Export citation
On a Mertens-type conjecture for number fields
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 177 / Issue 3 / November 2024
- Published online by Cambridge University Press:
- 19 December 2024, pp. 481-523
- Print publication:
- November 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON A CONJECTURE ON SHIFTED PRIMES WITH LARGE PRIME FACTORS, II
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 111 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 13 September 2024, pp. 48-55
- Print publication:
- February 2025
-
- Article
- Export citation
ON A PROBLEM OF PONGSRIIAM ON THE SUM OF DIVISORS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 111 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 13 September 2024, pp. 13-18
- Print publication:
- February 2025
-
- Article
- Export citation
Multiplicative dependence of rational values modulo approximate finitely generated groups
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 177 / Issue 1 / July 2024
- Published online by Cambridge University Press:
- 19 September 2024, pp. 149-165
- Print publication:
- July 2024
-
- Article
- Export citation
The Failure of Galois Descent for p-Selmer Groups of Elliptic Curves
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 177 / Issue 1 / July 2024
- Published online by Cambridge University Press:
- 19 September 2024, pp. 185-218
- Print publication:
- July 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Theta functions, fourth moments of eigenforms and the sup-norm problem II
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 12 / 2024
- Published online by Cambridge University Press:
- 30 May 2024, e11
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A solution to the Erdős–Sárközy–Sós problem on asymptotic Sidon bases of order 3
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 6 / June 2024
- Published online by Cambridge University Press:
- 10 May 2024, pp. 1418-1432
- Print publication:
- June 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Weak approximation on the norm one torus
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 6 / June 2024
- Published online by Cambridge University Press:
- 06 May 2024, pp. 1304-1348
- Print publication:
- June 2024
-
- Article
- Export citation
Summation formulae of multiplicative functions over arithmetic progressions and applications
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 77 / Issue 4 / August 2025
- Published online by Cambridge University Press:
- 12 April 2024, pp. 1243-1270
- Print publication:
- August 2025
-
- Article
- Export citation
ON THE SET OF KRONECKER NUMBERS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 110 / Issue 2 / October 2024
- Published online by Cambridge University Press:
- 08 March 2024, pp. 262-270
- Print publication:
- October 2024
-
- Article
- Export citation