Refine listing
Actions for selected content:
243 results in 65Mxx
Long Time Behaviour of an Exponential Integrator for a Vlasov-Poisson System with Strong Magnetic Field
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 18 / Issue 2 / August 2015
- Published online by Cambridge University Press:
- 30 July 2015, pp. 263-296
- Print publication:
- August 2015
-
- Article
- Export citation
GPU Accelerated Discontinuous Galerkin Methods for Shallow Water Equations
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 18 / Issue 1 / July 2015
- Published online by Cambridge University Press:
- 03 July 2015, pp. 37-64
- Print publication:
- July 2015
-
- Article
- Export citation
A Model of a Quantum Particle in a Quantum Environment: A Numerical Study
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 18 / Issue 1 / July 2015
- Published online by Cambridge University Press:
- 03 July 2015, pp. 247-262
- Print publication:
- July 2015
-
- Article
- Export citation
The Role of Inertia and Dissipation in the Dynamics of the Director for a Nematic Liquid Crystal Coupled with an Electric Field
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 18 / Issue 1 / July 2015
- Published online by Cambridge University Press:
- 03 July 2015, pp. 147-166
- Print publication:
- July 2015
-
- Article
- Export citation
Modeling 3D Magma Dynamics Using a Discontinuous Galerkin Method
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 18 / Issue 1 / July 2015
- Published online by Cambridge University Press:
- 03 July 2015, pp. 230-246
- Print publication:
- July 2015
-
- Article
- Export citation
Numerical Simulation for Moving Contact Line with Continuous Finite Element Schemes
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 18 / Issue 1 / July 2015
- Published online by Cambridge University Press:
- 03 July 2015, pp. 180-202
- Print publication:
- July 2015
-
- Article
- Export citation
Bespoke finite difference schemes that preserve multiple conservation laws
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 18 / Issue 1 / 2015
- Published online by Cambridge University Press:
- 01 May 2015, pp. 372-403
-
- Article
-
- You have access
- Export citation
ESTIMATES FOR SOLUTIONS TO DISCRETE CONVOLUTION EQUATIONS
- Part of
-
- Journal:
- Mathematika / Volume 61 / Issue 2 / May 2015
- Published online by Cambridge University Press:
- 15 April 2015, pp. 295-308
- Print publication:
- May 2015
-
- Article
- Export citation
Piecewise Legendre spectral-collocation method for Volterra integro-differential equations
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 18 / Issue 1 / 2015
- Published online by Cambridge University Press:
- 01 April 2015, pp. 231-249
-
- Article
-
- You have access
- Export citation
FOURTH-ORDER NUMERICAL METHODS FOR THE COUPLED KORTEWEG–DE VRIES EQUATIONS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 56 / Issue 3 / January 2015
- Published online by Cambridge University Press:
- 16 March 2015, pp. 275-285
-
- Article
-
- You have access
- Export citation
OPTIMAL
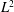 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}L^2$ ESTIMATES FOR THE SEMIDISCRETE GALERKIN METHOD APPLIED TO PARABOLIC INTEGRO-DIFFERENTIAL EQUATIONS WITH NONSMOOTH DATA
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}L^2$ ESTIMATES FOR THE SEMIDISCRETE GALERKIN METHOD APPLIED TO PARABOLIC INTEGRO-DIFFERENTIAL EQUATIONS WITH NONSMOOTH DATA
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 55 / Issue 3 / January 2014
- Published online by Cambridge University Press:
- 05 June 2014, pp. 245-266
-
- Article
-
- You have access
- Export citation
BLOW-UP OF THE NONEQUIVARIANT (
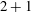 $2+1$)-DIMENSIONAL WAVE MAP
$2+1$)-DIMENSIONAL WAVE MAP
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 55 / Issue 2 / October 2013
- Published online by Cambridge University Press:
- 18 March 2014, pp. 151-161
-
- Article
-
- You have access
- Export citation
GEGENBAUER COLLOCATION INTEGRATION METHODS: ADVANCES IN COMPUTATIONAL OPTIMAL CONTROL THEORY
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 89 / Issue 1 / February 2014
- Published online by Cambridge University Press:
- 05 February 2014, pp. 168-170
- Print publication:
- February 2014
-
- Article
-
- You have access
- Export citation
A STUDY OF WELL-BALANCED FINITE VOLUME METHODS AND REFINEMENT INDICATORS FOR THE SHALLOW WATER EQUATIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 88 / Issue 2 / October 2013
- Published online by Cambridge University Press:
- 04 September 2013, pp. 351-352
- Print publication:
- October 2013
-
- Article
-
- You have access
- Export citation
Probabilistic Methods for the Incompressible Navier–Stokes Equations With Space Periodic Conditions
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 45 / Issue 3 / September 2013
- Published online by Cambridge University Press:
- 04 January 2016, pp. 742-772
- Print publication:
- September 2013
-
- Article
-
- You have access
- Export citation
AN IMPROVED SECOND-ORDER NUMERICAL METHOD FOR THE GENERALIZED BURGERS–FISHER EQUATION
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 54 / Issue 3 / January 2013
- Published online by Cambridge University Press:
- 12 June 2013, pp. 181-199
-
- Article
-
- You have access
- Export citation
ITERATIVE SOLUTION OF SHIFTED POSITIVE-DEFINITE LINEAR SYSTEMS ARISING IN A NUMERICAL METHOD FOR THE HEAT EQUATION BASED ON LAPLACE TRANSFORMATION AND QUADRATURE
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 53 / Issue 2 / October 2011
- Published online by Cambridge University Press:
- 15 August 2012, pp. 134-155
-
- Article
-
- You have access
- Export citation
NEW EXACT SOLUTIONS OF COUPLED (2+1)-DIMENSIONAL NONLINEAR SYSTEMS OF SCHRÖDINGER EQUATIONS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 52 / Issue 1 / July 2010
- Published online by Cambridge University Press:
- 03 May 2011, pp. 110-121
-
- Article
-
- You have access
- Export citation
A NOTE ON THE NUMERICAL APPROACH FOR THE REACTION–DIFFUSION PROBLEM WITH A FREE BOUNDARY CONDITION
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 51 / Issue 3 / January 2010
- Published online by Cambridge University Press:
- 13 October 2010, pp. 317-330
-
- Article
-
- You have access
- Export citation
ITERATED LAVRENTIEV REGULARIZATION FOR NONLINEAR ILL-POSED PROBLEMS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 51 / Issue 2 / October 2009
- Published online by Cambridge University Press:
- 19 April 2010, pp. 191-217
-
- Article
-
- You have access
- Export citation
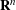
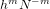
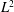
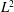
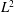
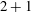
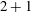
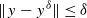 resulting in the convergence of the method as
resulting in the convergence of the method as 