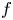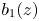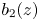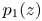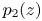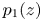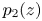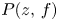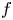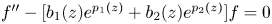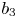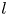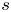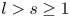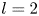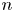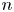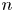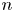Refine listing
Actions for selected content:
105 results in 34Bxx
Characterization of some convex curves on the 3-sphere
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society , First View
- Published online by Cambridge University Press:
- 06 October 2025, pp. 1-21
-
- Article
- Export citation
A unified topological analysis of variable growth Kirchhoff-type equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 09 September 2025, pp. 1-30
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Atypical bifurcation for periodic solutions of ϕ-Laplacian systems
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 03 September 2025, pp. 1-27
-
- Article
- Export citation
Multiple solutions to relativistic systems with potential boundary conditions
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society , First View
- Published online by Cambridge University Press:
- 01 September 2025, pp. 1-14
-
- Article
- Export citation
Spectral identities for Schrödinger operators
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 2 / June 2025
- Published online by Cambridge University Press:
- 13 January 2025, pp. 484-491
- Print publication:
- June 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Discounted optimal stopping zero-sum games in diffusion type models with maxima and minima
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 57 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 03 December 2024, pp. 241-270
- Print publication:
- March 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A unified characterization of convolution coefficients in nonlocal differential equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 18 September 2024, pp. 1-19
-
- Article
- Export citation
Optimal inverse problems of potentials for two given eigenvalues of Sturm–Liouville problems
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 07 March 2024, pp. 1-24
-
- Article
- Export citation
The lower bounds of non-real eigenvalues for singular indefinite Sturm–Liouville problems
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 155 / Issue 3 / June 2025
- Published online by Cambridge University Press:
- 22 December 2023, pp. 1051-1060
- Print publication:
- June 2025
-
- Article
- Export citation
Asymptotic formulas of the eigenvalues for the linearization of the scalar field equation
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 155 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 11 September 2023, pp. 307-344
- Print publication:
- February 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On classification of singular matrix difference equations of mixed order
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 4 / August 2024
- Published online by Cambridge University Press:
- 11 August 2023, pp. 1235-1258
- Print publication:
- August 2024
-
- Article
- Export citation
On the oscillation of certain second-order linear differential equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 6 / December 2023
- Published online by Cambridge University Press:
- 09 December 2022, pp. 1965-1992
- Print publication:
- December 2023
-
- Article
- Export citation
A modelling framework for efficient reduced order simulations of parametrised lithium-ion battery cells
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 34 / Issue 3 / June 2023
- Published online by Cambridge University Press:
- 29 November 2022, pp. 554-591
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Friedrichs extensions for Sturm–Liouville operators with complex coefficients and their spectra
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 6 / December 2023
- Published online by Cambridge University Press:
- 18 November 2022, pp. 1883-1905
- Print publication:
- December 2023
-
- Article
- Export citation
Singular boundary conditions for Sturm–Liouville operators via perturbation theory
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 4 / August 2023
- Published online by Cambridge University Press:
- 23 June 2022, pp. 1110-1146
- Print publication:
- August 2023
-
- Article
- Export citation
SOLUTIONS TO DIFFERENTIAL EQUATIONS VIA FIXED POINT APPROACHES: NEW MATHEMATICAL FOUNDATIONS AND APPLICATIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 1 / August 2022
- Published online by Cambridge University Press:
- 09 June 2022, pp. 163-164
- Print publication:
- August 2022
-
- Article
-
- You have access
- HTML
- Export citation
Steady states of thin-film equations with van der Waals force with mass constraint
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 34 / Issue 2 / April 2023
- Published online by Cambridge University Press:
- 30 May 2022, pp. 280-302
-
- Article
- Export citation
THREE-DIMENSIONAL ANALYTICAL SOLUTION OF THE ADVECTION-DIFFUSION EQUATION FOR AIR POLLUTION DISPERSION
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 64 / Issue 1 / January 2022
- Published online by Cambridge University Press:
- 26 April 2022, pp. 40-53
-
- Article
- Export citation
Jump phenomena of the n-th eigenvalue of discrete Sturm–Liouville problems with application to the continuous case
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 2 / April 2023
- Published online by Cambridge University Press:
- 02 March 2022, pp. 619-653
- Print publication:
- April 2023
-
- Article
- Export citation
Periodic solutions of p-Laplacian differential equations with jumping nonlinearity across half-eigenvalues
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 07 January 2022, pp. 307-326
- Print publication:
- February 2023
-
- Article
- Export citation