Refine listing
Actions for selected content:
182 results in 60Bxx
Trees with random conductivities and the (reciprocal) inverse Gaussian distribution
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 30 / Issue 2 / June 1998
- Published online by Cambridge University Press:
- 01 July 2016, pp. 409-424
- Print publication:
- June 1998
-
- Article
- Export citation
Integral Probability Metrics and Their Generating Classes of Functions
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 29 / Issue 2 / June 1997
- Published online by Cambridge University Press:
- 01 July 2016, pp. 429-443
- Print publication:
- June 1997
-
- Article
- Export citation
Stochastic Orders Generated by Integrals: a Unified Study
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 29 / Issue 2 / June 1997
- Published online by Cambridge University Press:
- 01 July 2016, pp. 414-428
- Print publication:
- June 1997
-
- Article
- Export citation
Compound Poisson limit theorems for Markov chains
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 34 / Issue 1 / March 1997
- Published online by Cambridge University Press:
- 14 July 2016, pp. 24-34
- Print publication:
- March 1997
-
- Article
- Export citation
Non-explosivity of limits of conditioned birth and death processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 34 / Issue 1 / March 1997
- Published online by Cambridge University Press:
- 14 July 2016, pp. 35-45
- Print publication:
- March 1997
-
- Article
- Export citation
Exponentially bounded positive-definite functions on a commutative hypergroup
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 61 / Issue 2 / October 1996
- Published online by Cambridge University Press:
- 09 April 2009, pp. 238-248
- Print publication:
- October 1996
-
- Article
-
- You have access
- Export citation
Asymptotic distributions for the Ehrenfest urn and related random walks
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 33 / Issue 2 / September 1996
- Published online by Cambridge University Press:
- 14 July 2016, pp. 340-356
- Print publication:
- September 1996
-
- Article
- Export citation
Multivariate normal approximations by Stein's method and size bias couplings
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 33 / Issue 1 / March 1996
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1-17
- Print publication:
- March 1996
-
- Article
- Export citation
Weak convergence of conditioned processes on a countable state space
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 32 / Issue 4 / December 1995
- Published online by Cambridge University Press:
- 14 July 2016, pp. 902-916
- Print publication:
- December 1995
-
- Article
- Export citation
On weak convergence within a Lorenz ordering family of distributions
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 32 / Issue 4 / December 1995
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1028-1031
- Print publication:
- December 1995
-
- Article
- Export citation
Limit laws for a stochastic process and random recursion arising in probabilistic modelling
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 27 / Issue 1 / March 1995
- Published online by Cambridge University Press:
- 01 July 2016, pp. 185-202
- Print publication:
- March 1995
-
- Article
- Export citation
An L 2 convergence theorem for random affine mappings
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 32 / Issue 1 / March 1995
- Published online by Cambridge University Press:
- 14 July 2016, pp. 183-192
- Print publication:
- March 1995
-
- Article
- Export citation
Estimating the home range
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 31 / Issue 3 / September 1994
- Published online by Cambridge University Press:
- 14 July 2016, pp. 700-720
- Print publication:
- September 1994
-
- Article
- Export citation
Approach to Stationarity of the Bernoulli–Laplace Diffusion Model
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 26 / Issue 3 / September 1994
- Published online by Cambridge University Press:
- 01 July 2016, pp. 715-727
- Print publication:
- September 1994
-
- Article
- Export citation
A Note on Electrical Networks and the Inverse Gaussian Distribution
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 26 / Issue 1 / March 1994
- Published online by Cambridge University Press:
- 01 July 2016, pp. 63-67
- Print publication:
- March 1994
-
- Article
- Export citation
Quasi-limiting distributions of Markov chains that are skip-free to the left in continuous time
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 30 / Issue 3 / September 1993
- Published online by Cambridge University Press:
- 14 July 2016, pp. 509-517
- Print publication:
- September 1993
-
- Article
- Export citation
Asymptotic stationarity of multichannel queues
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 25 / Issue 1 / March 1993
- Published online by Cambridge University Press:
- 01 July 2016, pp. 203-220
- Print publication:
- March 1993
-
- Article
- Export citation
On the number of real roots of a random algebraic equation
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 54 / Issue 1 / February 1993
- Published online by Cambridge University Press:
- 09 April 2009, pp. 86-96
- Print publication:
- February 1993
-
- Article
-
- You have access
- Export citation
Factorization of probability measures on symmetric hypergroups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 50 / Issue 3 / June 1991
- Published online by Cambridge University Press:
- 09 April 2009, pp. 417-467
- Print publication:
- June 1991
-
- Article
-
- You have access
- Export citation
Coin tossing and sum sets
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 43 / Issue 2 / October 1987
- Published online by Cambridge University Press:
- 09 April 2009, pp. 211-219
- Print publication:
- October 1987
-
- Article
-
- You have access
- Export citation
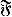 of functions and probability measures
of functions and probability measures 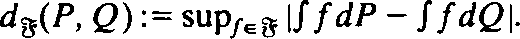 A unified study of such
A unified study of such 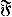 be a class of functions and let
be a class of functions and let 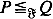 , if ∫ ⨍
, if ∫ ⨍ 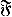 . Marshall (1991) posed the problem of characterizing the maximal cone of functions generating such an ordering. We solve this problem by using methods from functional analysis. Another purpose of this paper is to derive properties of such
. Marshall (1991) posed the problem of characterizing the maximal cone of functions generating such an ordering. We solve this problem by using methods from functional analysis. Another purpose of this paper is to derive properties of such 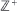 with absorption at zero and suppose that
with absorption at zero and suppose that 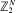 in continuous time
in continuous time 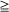 0 can be expressed in terms of binomial distributions; their limit behaviour for
0 can be expressed in terms of binomial distributions; their limit behaviour for 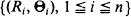 are the polar coordinates of the sightings, then is a sup-measure and corresponds to the right endpoint of the distribution
are the polar coordinates of the sightings, then is a sup-measure and corresponds to the right endpoint of the distribution 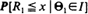 . The corresponding upper semi-continuous function
. The corresponding upper semi-continuous function 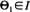 is in the domain of attraction of an extreme value distribution with bounded support, we are able to give an approximate confidence region.
is in the domain of attraction of an extreme value distribution with bounded support, we are able to give an approximate confidence region.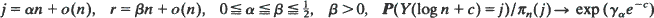 as
as 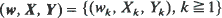 where
where 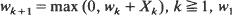 is a vector in
is a vector in 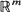 with non-negative coordinates,
with non-negative coordinates, 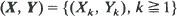 is an
is an 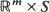 -valued process,
-valued process, 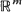 are meant in the coordinate-wise sense. It is shown that a type of asymptotic stationarity of (
are meant in the coordinate-wise sense. It is shown that a type of asymptotic stationarity of (