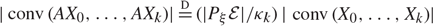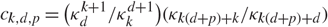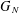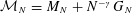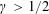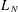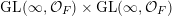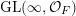Refine listing
Actions for selected content:
182 results in 60Bxx
The De Vylder–Goovaerts conjecture holds within the diffusion limit
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 56 / Issue 2 / June 2019
- Published online by Cambridge University Press:
- 30 July 2019, pp. 546-557
- Print publication:
- June 2019
-
- Article
- Export citation
Discrete derivative asymptotics of the β-Hermite eigenvalues
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 28 / Issue 5 / September 2019
- Published online by Cambridge University Press:
- 17 April 2019, pp. 657-674
-
- Article
- Export citation
RANDOM MATRICES WITH SLOW CORRELATION DECAY
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 7 / 2019
- Published online by Cambridge University Press:
- 26 March 2019, e8
-
- Article
-
- You have access
- Open access
- Export citation
Random affine simplexes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 56 / Issue 1 / March 2019
- Published online by Cambridge University Press:
- 12 July 2019, pp. 39-51
- Print publication:
- March 2019
-
- Article
- Export citation
Diffusion approximations for load balancing mechanisms in cloud storage systems
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 51 / Issue 1 / March 2019
- Published online by Cambridge University Press:
- 22 July 2019, pp. 41-86
- Print publication:
- March 2019
-
- Article
- Export citation
REGULARIZATION OF NON-NORMAL MATRICES BY GAUSSIAN NOISE—THE BANDED TOEPLITZ AND TWISTED TOEPLITZ CASES
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 7 / 2019
- Published online by Cambridge University Press:
- 13 February 2019, e3
-
- Article
-
- You have access
- Open access
- Export citation
Freeness and The Partial Transposes of Wishart Random Matrices
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 71 / Issue 3 / June 2019
- Published online by Cambridge University Press:
- 09 January 2019, pp. 659-681
- Print publication:
- June 2019
-
- Article
-
- You have access
- Export citation
Uniform decomposition of probability measures: quantization, clustering and rate of convergence
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 55 / Issue 4 / December 2018
- Published online by Cambridge University Press:
- 16 January 2019, pp. 1037-1045
- Print publication:
- December 2018
-
- Article
- Export citation
A Combinatorial Approach to Small Ball Inequalities for Sums and Differences
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 28 / Issue 1 / January 2019
- Published online by Cambridge University Press:
- 06 November 2018, pp. 100-129
-
- Article
- Export citation
From trees to graphs: collapsing continuous-time branching processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 55 / Issue 3 / September 2018
- Published online by Cambridge University Press:
- 16 November 2018, pp. 900-919
- Print publication:
- September 2018
-
- Article
- Export citation
Large deviations for randomly connected neural networks: II. State-dependent interactions
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 50 / Issue 3 / September 2018
- Published online by Cambridge University Press:
- 16 November 2018, pp. 983-1004
- Print publication:
- September 2018
-
- Article
- Export citation
Large deviations for randomly connected neural networks: I. Spatially extended systems
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 50 / Issue 3 / September 2018
- Published online by Cambridge University Press:
- 16 November 2018, pp. 944-982
- Print publication:
- September 2018
-
- Article
- Export citation
COMPARISON OF WEAK AND STRONG MOMENTS FOR VECTORS WITH INDEPENDENT COORDINATES
- Part of
-
- Journal:
- Mathematika / Volume 64 / Issue 1 / 2018
- Published online by Cambridge University Press:
- 14 February 2018, pp. 211-229
- Print publication:
- 2018
-
- Article
- Export citation
Uniform convergence of conditional distributions for absorbed one-dimensional diffusions
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 50 / Issue 1 / March 2018
- Published online by Cambridge University Press:
- 20 March 2018, pp. 178-203
- Print publication:
- March 2018
-
- Article
- Export citation
Ergodic measures on spaces of infinite matrices over non-Archimedean locally compact fields
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 12 / December 2017
- Published online by Cambridge University Press:
- 11 September 2017, pp. 2482-2533
- Print publication:
- December 2017
-
- Article
-
- You have access
- HTML
- Export citation
A spectral method for community detection in moderately sparse degree-corrected stochastic block models
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 49 / Issue 3 / September 2017
- Published online by Cambridge University Press:
- 08 September 2017, pp. 686-721
- Print publication:
- September 2017
-
- Article
- Export citation
Local limits of Galton–Watson trees conditioned on the number of protected nodes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 54 / Issue 1 / March 2017
- Published online by Cambridge University Press:
- 04 April 2017, pp. 55-65
- Print publication:
- March 2017
-
- Article
- Export citation
Nonuniversality of weighted random graphs with infinite variance degree
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 54 / Issue 1 / March 2017
- Published online by Cambridge University Press:
- 04 April 2017, pp. 146-164
- Print publication:
- March 2017
-
- Article
- Export citation
Asymptotics for randomly reinforced urns with random barriers
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 53 / Issue 4 / December 2016
- Published online by Cambridge University Press:
- 09 December 2016, pp. 1206-1220
- Print publication:
- December 2016
-
- Article
- Export citation
Synchronization and fluctuation theorems for interacting Friedman urns
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 53 / Issue 4 / December 2016
- Published online by Cambridge University Press:
- 09 December 2016, pp. 1221-1239
- Print publication:
- December 2016
-
- Article
- Export citation