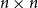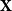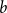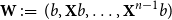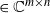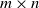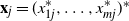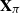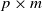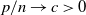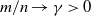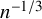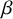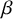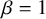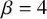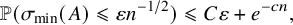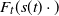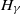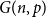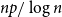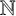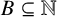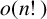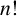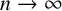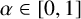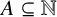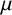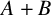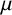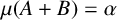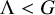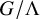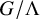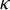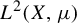Refine listing
Actions for selected content:
182 results in 60Bxx
Cokernel statistics for walk matrices of directed and weighted random graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 34 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 18 October 2024, pp. 131-150
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Partial recovery and weak consistency in the non-uniform hypergraph stochastic block model
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 34 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 09 October 2024, pp. 1-51
-
- Article
- Export citation
The full rank condition for sparse random matrices
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 33 / Issue 5 / September 2024
- Published online by Cambridge University Press:
- 20 September 2024, pp. 643-707
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The limiting spectral distribution of large random permutation matrices
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 12 April 2024, pp. 1301-1318
- Print publication:
- December 2024
-
- Article
- Export citation
Asymptotic expansions relating to the distribution of the length of longest increasing subsequences
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 15 March 2024, e36
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
THERMODYNAMIC FORMALISM FOR AMENABLE GROUPS AND COUNTABLE STATE SPACES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 6 / November 2024
- Published online by Cambridge University Press:
- 15 March 2024, pp. 2647-2711
- Print publication:
- November 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Asymptotic expansion of
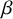 $\beta $ matrix models in the multi-cut regime
$\beta $ matrix models in the multi-cut regime
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 24 January 2024, e13
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The least singular value of a random symmetric matrix
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 12 / 2024
- Published online by Cambridge University Press:
- 23 January 2024, e3
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Max-linear graphical models with heavy-tailed factors on trees of transitive tournaments
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 56 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 15 December 2023, pp. 621-665
- Print publication:
- June 2024
-
- Article
- Export citation
Local convergence of critical Galton–Watson trees
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 30 November 2023, pp. 851-857
- Print publication:
- September 2024
-
- Article
- Export citation
From topological recursion to wave functions and PDEs quantizing hyperelliptic curves
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 31 October 2023, e99
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Autocorrelations of characteristic polynomials for the Alternative Circular Unitary Ensemble
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 66 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 27 October 2023, pp. 51-64
- Print publication:
- January 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Gaussian fluctuations in the equipartition principle for Wigner matrices
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 23 August 2023, e74
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Strong convergence of peaks over a threshold
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 23 August 2023, pp. 529-539
- Print publication:
- June 2024
-
- Article
- Export citation
Limiting empirical spectral distribution for the non-backtracking matrix of an Erdős-Rényi random graph
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 6 / November 2023
- Published online by Cambridge University Press:
- 31 July 2023, pp. 956-973
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Phase transition for the generalized two-community stochastic block model
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 31 July 2023, pp. 385-400
- Print publication:
- June 2024
-
- Article
- Export citation
ON THE DENSITY OF SUMSETS, II
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 3 / June 2024
- Published online by Cambridge University Press:
- 17 July 2023, pp. 414-419
- Print publication:
- June 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Expanding measures: Random walks and rigidity on homogeneous spaces
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 04 July 2023, e59
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Wasserstein convergence rates in the invariance principle for deterministic dynamical systems
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 4 / April 2024
- Published online by Cambridge University Press:
- 13 June 2023, pp. 1172-1191
- Print publication:
- April 2024
-
- Article
- Export citation
On the spectral theory of groups of automorphisms of S-adic nilmanifolds
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 3 / March 2024
- Published online by Cambridge University Press:
- 29 May 2023, pp. 705-726
- Print publication:
- March 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation