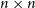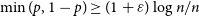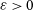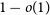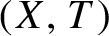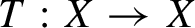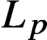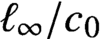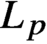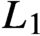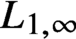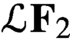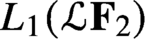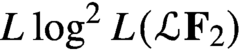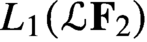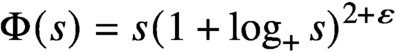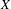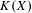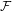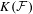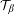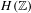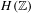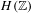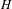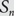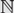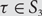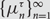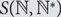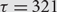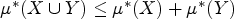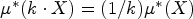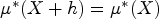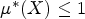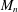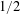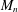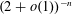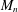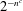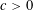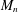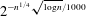Refine listing
Actions for selected content:
182 results in 60Bxx
Asymptotic behavior of the weak approximation to a class of Gaussian processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 58 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 16 September 2021, pp. 693-707
- Print publication:
- September 2021
-
- Article
- Export citation
Spectral gap in random bipartite biregular graphs and applications
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 31 / Issue 2 / March 2022
- Published online by Cambridge University Press:
- 23 July 2021, pp. 229-267
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Singularity of sparse random matrices: simple proofs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 31 / Issue 1 / January 2022
- Published online by Cambridge University Press:
- 15 June 2021, pp. 21-28
-
- Article
- Export citation
Equipartition principle for Wigner matrices
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 27 May 2021, e44
-
- Article
-
- You have access
- Open access
- Export citation
Optimal group testing
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 30 / Issue 6 / November 2021
- Published online by Cambridge University Press:
- 28 January 2021, pp. 811-848
-
- Article
- Export citation
Uniformly positive entropy of induced transformations
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 1 / January 2022
- Published online by Cambridge University Press:
- 28 December 2020, pp. 9-18
- Print publication:
- January 2022
-
- Article
- Export citation
Noncommutative strong maximals and almost uniform convergence in several directions
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 8 / 2020
- Published online by Cambridge University Press:
- 20 November 2020, e57
-
- Article
-
- You have access
- Open access
- Export citation
Spread out random walks on homogeneous spaces
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 11 / November 2021
- Published online by Cambridge University Press:
- 06 October 2020, pp. 3439-3473
- Print publication:
- November 2021
-
- Article
- Export citation
Resilience of the rank of random matrices
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 30 / Issue 2 / March 2021
- Published online by Cambridge University Press:
- 28 August 2020, pp. 163-174
-
- Article
- Export citation
Positive definite functions and cut-off for discrete groups
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 2 / June 2021
- Published online by Cambridge University Press:
- 22 June 2020, pp. 306-322
- Print publication:
- June 2021
-
- Article
- Export citation
GAMES AND HEREDITARY BAIRENESS IN HYPERSPACES AND SPACES OF PROBABILITY MEASURES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 3 / May 2022
- Published online by Cambridge University Press:
- 15 June 2020, pp. 851-868
- Print publication:
- May 2022
-
- Article
- Export citation
Smale endomorphisms over graph-directed Markov systems
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 8 / August 2021
- Published online by Cambridge University Press:
- 08 June 2020, pp. 2508-2541
- Print publication:
- August 2021
-
- Article
- Export citation
HALF-SPACE MACDONALD PROCESSES
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 8 / 2020
- Published online by Cambridge University Press:
- 26 May 2020, e11
-
- Article
-
- You have access
- Open access
- Export citation
Unlabelled Gibbs partitions
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 29 / Issue 2 / March 2020
- Published online by Cambridge University Press:
- 04 November 2019, pp. 293-309
-
- Article
- Export citation
Non-triviality of the Poisson boundary of random walks on the group
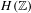 $H(\mathbb{Z})$ of Monod
$H(\mathbb{Z})$ of Monod
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 4 / April 2021
- Published online by Cambridge University Press:
- 04 November 2019, pp. 1160-1189
- Print publication:
- April 2021
-
- Article
- Export citation
The Infinite limit of random permutations avoiding patterns of length three
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 29 / Issue 1 / January 2020
- Published online by Cambridge University Press:
- 14 October 2019, pp. 137-152
-
- Article
- Export citation
Limit theorems for multivariate Brownian semistationary processes and feasible results
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 51 / Issue 3 / September 2019
- Published online by Cambridge University Press:
- 03 September 2019, pp. 667-716
- Print publication:
- September 2019
-
- Article
- Export citation
On the notions of upper and lower density
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 63 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 30 August 2019, pp. 139-167
-
- Article
- Export citation
SINGULARITY OF RANDOM SYMMETRIC MATRICES—A COMBINATORIAL APPROACH TO IMPROVED BOUNDS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 7 / 2019
- Published online by Cambridge University Press:
- 02 August 2019, e22
-
- Article
-
- You have access
- Open access
- Export citation
Skew product Smale endomorphisms over countable shifts of finite type
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 11 / November 2020
- Published online by Cambridge University Press:
- 25 June 2019, pp. 3105-3149
- Print publication:
- November 2020
-
- Article
- Export citation