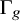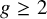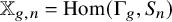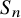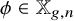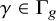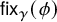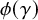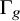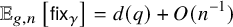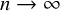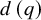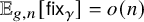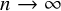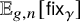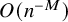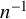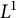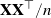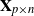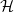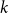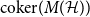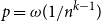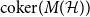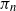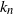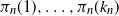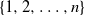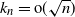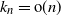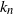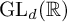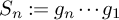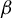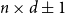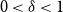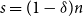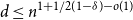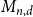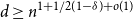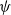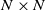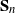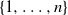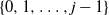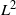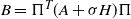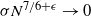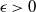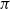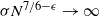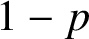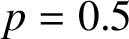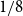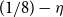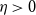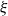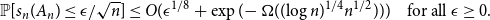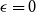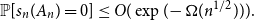Refine listing
Actions for selected content:
182 results in 60Bxx
The Asymptotic Statistics of Random Covering Surfaces
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 11 / 2023
- Published online by Cambridge University Press:
- 15 May 2023, e15
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Strong Shannon–McMillan–Breiman’s theorem for locally compact groups
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 05 May 2023, pp. 1274-1279
- Print publication:
- December 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Large deviations of extremal eigenvalues of sample covariance matrices
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 24 April 2023, pp. 1275-1280
- Print publication:
- December 2023
-
- Article
- Export citation
Abelian groups from random hypergraphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 4 / July 2023
- Published online by Cambridge University Press:
- 20 April 2023, pp. 654-664
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Asymptotic behaviour of the first positions of uniform parking functions
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 20 April 2023, pp. 1201-1218
- Print publication:
- December 2023
-
- Article
- Export citation
Local limits of spatial inhomogeneous random graphs
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 55 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 14 April 2023, pp. 793-840
- Print publication:
- September 2023
-
- Article
- Export citation
BERRY–ESSEEN BOUND AND LOCAL LIMIT THEOREM FOR THE COEFFICIENTS OF PRODUCTS OF RANDOM MATRICES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 2 / March 2024
- Published online by Cambridge University Press:
- 07 December 2022, pp. 705-735
- Print publication:
- March 2024
-
- Article
- Export citation
The natural extension of the random beta-transformation
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 11 / November 2023
- Published online by Cambridge University Press:
- 04 November 2022, pp. 3861-3896
- Print publication:
- November 2023
-
- Article
- Export citation
Rank-uniform local law for Wigner matrices
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 27 October 2022, e96
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A transport process on graphs and its limiting distributions
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 10 October 2022, pp. 341-357
- Print publication:
- March 2023
-
- Article
- Export citation
Sparse recovery properties of discrete random matrices
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 2 / March 2023
- Published online by Cambridge University Press:
- 04 October 2022, pp. 316-325
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Exponential convergence to a quasi-stationary distribution for birth–death processes with an entrance boundary at infinity
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 59 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 10 August 2022, pp. 983-991
- Print publication:
- December 2022
-
- Article
- Export citation
A unifying approach to non-minimal quasi-stationary distributions for one-dimensional diffusions
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 59 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 08 August 2022, pp. 1106-1128
- Print publication:
- December 2022
-
- Article
- Export citation
On the moments of characteristic polynomials
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 65 / Issue S1 / May 2023
- Published online by Cambridge University Press:
- 05 August 2022, pp. S102-S122
- Print publication:
- May 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The hit-and-run version of top-to-random
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 59 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 12 July 2022, pp. 860-879
- Print publication:
- September 2022
-
- Article
- Export citation
Spectral alignment of correlated Gaussian matrices
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 54 / Issue 1 / March 2022
- Published online by Cambridge University Press:
- 28 January 2022, pp. 279-310
- Print publication:
- March 2022
-
- Article
- Export citation
On model selection for dense stochastic block models
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 54 / Issue 1 / March 2022
- Published online by Cambridge University Press:
- 14 January 2022, pp. 202-226
- Print publication:
- March 2022
-
- Article
- Export citation
SMALL-SCALE EQUIDISTRIBUTION OF RANDOM WAVES GENERATED BY AN UNFAIR COIN FLIP
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 114 / Issue 2 / April 2023
- Published online by Cambridge University Press:
- 29 November 2021, pp. 222-252
- Print publication:
- April 2023
-
- Article
- Export citation
Large-deviation asymptotics of condition numbers of random matrices
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 58 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 22 November 2021, pp. 1114-1130
- Print publication:
- December 2021
-
- Article
- Export citation
On the smallest singular value of symmetric random matrices
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 31 / Issue 4 / July 2022
- Published online by Cambridge University Press:
- 05 November 2021, pp. 662-683
-
- Article
- Export citation