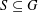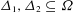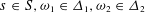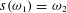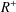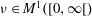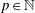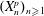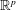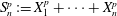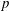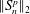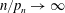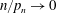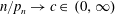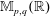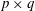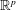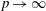Refine listing
Actions for selected content:
182 results in 60Bxx
On the evolution of topology in dynamic clique complexes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 48 / Issue 4 / December 2016
- Published online by Cambridge University Press:
- 11 January 2017, pp. 989-1014
- Print publication:
- December 2016
-
- Article
- Export citation
Central limit theorems for a hypergeometric randomly reinforced urn
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 53 / Issue 3 / September 2016
- Published online by Cambridge University Press:
- 24 October 2016, pp. 899-913
- Print publication:
- September 2016
-
- Article
- Export citation
QUASIRANDOM GROUP ACTIONS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 4 / 2016
- Published online by Cambridge University Press:
- 30 August 2016, e24
-
- Article
-
- You have access
- Open access
- Export citation
On a memory game and preferential attachment graphs
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 48 / Issue 2 / June 2016
- Published online by Cambridge University Press:
- 10 June 2016, pp. 585-609
- Print publication:
- June 2016
-
- Article
- Export citation
Coupling on weighted branching trees
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 48 / Issue 2 / June 2016
- Published online by Cambridge University Press:
- 10 June 2016, pp. 499-524
- Print publication:
- June 2016
-
- Article
- Export citation
Escape from the boundary in Markov population processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 47 / Issue 4 / December 2015
- Published online by Cambridge University Press:
- 21 March 2016, pp. 1190-1211
- Print publication:
- December 2015
-
- Article
-
- You have access
- Export citation
Reversible Markov structures on divisible set partitions
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 52 / Issue 3 / September 2015
- Published online by Cambridge University Press:
- 30 March 2016, pp. 622-635
- Print publication:
- September 2015
-
- Article
-
- You have access
- Export citation
The Satisfiability Threshold for k-XORSAT
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 25 / Issue 2 / March 2016
- Published online by Cambridge University Press:
- 31 July 2015, pp. 236-268
-
- Article
- Export citation
A Numerical Lower Bound for the Spectral Radius of Random Walks on Surface Groups
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 24 / Issue 6 / November 2015
- Published online by Cambridge University Press:
- 29 January 2015, pp. 838-856
-
- Article
- Export citation
STABLE AND SEMISTABLE PROBABILITY MEASURES ON CONVEX CONE
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 98 / Issue 3 / June 2015
- Published online by Cambridge University Press:
- 20 November 2014, pp. 390-406
- Print publication:
- June 2015
-
- Article
-
- You have access
- Export citation
Krein-Smulian-Type Theorems
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 58 / Issue 2 / June 2015
- Published online by Cambridge University Press:
- 24 October 2014, pp. 441-444
-
- Article
-
- You have access
- Export citation
Existence and Uniqueness of a Quasistationary Distribution for Markov Processes with Fast Return from Infinity
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 51 / Issue 3 / September 2014
- Published online by Cambridge University Press:
- 30 January 2018, pp. 756-768
- Print publication:
- September 2014
-
- Article
-
- You have access
- Export citation
LIMIT THEOREMS FOR RADIAL RANDOM WALKS ON EUCLIDEAN SPACES OF HIGH DIMENSIONS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 97 / Issue 2 / October 2014
- Published online by Cambridge University Press:
- 25 July 2014, pp. 212-236
- Print publication:
- October 2014
-
- Article
-
- You have access
- Export citation
Improved Approximation of the Sum of Random Vectors by the Skew Normal Distribution
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 51 / Issue 2 / June 2014
- Published online by Cambridge University Press:
- 19 February 2016, pp. 466-482
- Print publication:
- June 2014
-
- Article
-
- You have access
- Export citation
A Characterisation of Transient Random Walks on Stochastic Matrices with Dirichlet Distributed Limits
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 51 / Issue 2 / June 2014
- Published online by Cambridge University Press:
- 19 February 2016, pp. 542-555
- Print publication:
- June 2014
-
- Article
-
- You have access
- Export citation
Emergent Structures in Large Networks
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 50 / Issue 3 / September 2013
- Published online by Cambridge University Press:
- 30 January 2018, pp. 883-888
- Print publication:
- September 2013
-
- Article
-
- You have access
- Export citation
ASPECTS OF RECURRENCE AND TRANSIENCE FOR LÉVY PROCESSES IN TRANSFORMATION GROUPS AND NONCOMPACT RIEMANNIAN SYMMETRIC PAIRS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 94 / Issue 3 / June 2013
- Published online by Cambridge University Press:
- 31 May 2013, pp. 304-320
- Print publication:
- June 2013
-
- Article
-
- You have access
- Export citation
Discrete-Time Semi-Markov Random Evolutions and their Applications
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 45 / Issue 1 / March 2013
- Published online by Cambridge University Press:
- 04 January 2016, pp. 214-240
- Print publication:
- March 2013
-
- Article
-
- You have access
- Export citation
Averaging for a Fully Coupled Piecewise-Deterministic Markov Process in Infinite Dimensions
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 44 / Issue 3 / September 2012
- Published online by Cambridge University Press:
- 04 January 2016, pp. 749-773
- Print publication:
- September 2012
-
- Article
-
- You have access
- Export citation
Probabilities of Competing Binomial Random Variables
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 49 / Issue 3 / September 2012
- Published online by Cambridge University Press:
- 04 February 2016, pp. 731-744
- Print publication:
- September 2012
-
- Article
-
- You have access
- Export citation