Refine listing
Actions for selected content:
181 results in 60Bxx
Some fluctuation identities for Lévy processes with jumps of the same sign
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 41 / Issue 4 / December 2004
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1191-1198
- Print publication:
- December 2004
-
- Article
- Export citation
Maximum dynamic entropy models
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 41 / Issue 2 / June 2004
- Published online by Cambridge University Press:
- 14 July 2016, pp. 379-390
- Print publication:
- June 2004
-
- Article
- Export citation
Boundedness of vector-valued martingale transforms on extreme points and applciations
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 76 / Issue 2 / April 2004
- Published online by Cambridge University Press:
- 09 April 2009, pp. 207-222
- Print publication:
- April 2004
-
- Article
-
- You have access
- Export citation
Optimal couplings are totally positive and more
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 41 / Issue A / 2004
- Published online by Cambridge University Press:
- 14 July 2016, pp. 321-332
- Print publication:
- 2004
-
- Article
- Export citation
Deterministic approximation of a stochastic metapopulation model
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 35 / Issue 3 / September 2003
- Published online by Cambridge University Press:
- 01 July 2016, pp. 691-720
- Print publication:
- September 2003
-
- Article
- Export citation
Discrete-time singularly perturbed Markov chains: aggregation, occupation measures, and switching diffusion limit
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 35 / Issue 2 / June 2003
- Published online by Cambridge University Press:
- 22 February 2016, pp. 449-476
- Print publication:
- June 2003
-
- Article
- Export citation
Frailty models based on Lévy processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 35 / Issue 2 / June 2003
- Published online by Cambridge University Press:
- 22 February 2016, pp. 532-550
- Print publication:
- June 2003
-
- Article
- Export citation
Limit theorems for isotropic random walks on triangle buildings
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 73 / Issue 3 / December 2002
- Published online by Cambridge University Press:
- 09 April 2009, pp. 301-334
- Print publication:
- December 2002
-
- Article
-
- You have access
- Export citation
A note on convergence of probability measures
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 38 / Issue 4 / December 2001
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1055-1058
- Print publication:
- December 2001
-
- Article
- Export citation
Generalized vector multiplicative cascades
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 33 / Issue 4 / December 2001
- Published online by Cambridge University Press:
- 01 July 2016, pp. 874-895
- Print publication:
- December 2001
-
- Article
- Export citation
Weakly approaching sequences of random distributions
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 37 / Issue 3 / September 2000
- Published online by Cambridge University Press:
- 14 July 2016, pp. 807-822
- Print publication:
- September 2000
-
- Article
- Export citation
Domain of attraction of the quasi-stationary distributions for the Ornstein-Uhlenbeck process
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 37 / Issue 2 / June 2000
- Published online by Cambridge University Press:
- 14 July 2016, pp. 511-520
- Print publication:
- June 2000
-
- Article
- Export citation
Asymptotic independence of counts in isotropic planar point processes of phase-type
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 32 / Issue 2 / June 2000
- Published online by Cambridge University Press:
- 01 July 2016, pp. 363-375
- Print publication:
- June 2000
-
- Article
- Export citation
Weak approximation for a class of Gaussian processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 37 / Issue 2 / June 2000
- Published online by Cambridge University Press:
- 14 July 2016, pp. 400-407
- Print publication:
- June 2000
-
- Article
- Export citation
The arithmetic of a semigroup of series of Walsh functions
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 68 / Issue 3 / June 2000
- Published online by Cambridge University Press:
- 09 April 2009, pp. 365-378
- Print publication:
- June 2000
-
- Article
-
- You have access
- Export citation
Analyticity of iterates of random non-expansive maps
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 32 / Issue 1 / March 2000
- Published online by Cambridge University Press:
- 01 July 2016, pp. 193-220
- Print publication:
- March 2000
-
- Article
- Export citation
Limiting conditional and conditional invariant distributions for the Poisson process with negative drift
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 36 / Issue 4 / December 1999
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1194-1209
- Print publication:
- December 1999
-
- Article
- Export citation
A recognition algorithm for non-generic classical groups over finite fields
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 67 / Issue 2 / October 1999
- Published online by Cambridge University Press:
- 09 April 2009, pp. 223-253
- Print publication:
- October 1999
-
- Article
-
- You have access
- Export citation
Random walks on finite semigroups
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 35 / Issue 4 / December 1998
- Published online by Cambridge University Press:
- 14 July 2016, pp. 824-832
- Print publication:
- December 1998
-
- Article
- Export citation
Trees with random conductivities and the (reciprocal) inverse Gaussian distribution
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 30 / Issue 2 / June 1998
- Published online by Cambridge University Press:
- 01 July 2016, pp. 409-424
- Print publication:
- June 1998
-
- Article
- Export citation
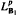 into
into 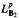 for some
for some 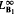 into
into 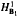 into
into 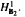 . Applications to
. Applications to 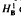 defined in the case of a general filtration has nice dense sets and nice atomic decompositions if and only if Β has the Radon-Nikodým property.
defined in the case of a general filtration has nice dense sets and nice atomic decompositions if and only if Β has the Radon-Nikodým property.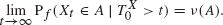
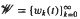 be the classical system of the Walsh functions,
be the classical system of the Walsh functions, 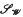 the multiplicative semigroup of the functions represented by series of functions
the multiplicative semigroup of the functions represented by series of functions 