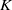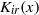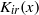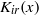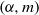Refine listing
Actions for selected content:
325 results in 26xxx
SOME INEQUALITIES OF JENSEN TYPE FOR ARG-SQUARE CONVEX FUNCTIONS OF UNITARY OPERATORS IN HILBERT SPACES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 90 / Issue 1 / August 2014
- Published online by Cambridge University Press:
- 12 May 2014, pp. 65-73
- Print publication:
- August 2014
-
- Article
-
- You have access
- Export citation
SOME RESULTS ON COMPARING TWO INTEGRAL MEANS FOR ABSOLUTELY CONTINUOUS FUNCTIONS AND APPLICATIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 90 / Issue 2 / October 2014
- Published online by Cambridge University Press:
- 10 April 2014, pp. 264-274
- Print publication:
- October 2014
-
- Article
-
- You have access
- Export citation
Fractional Discrete Processes: Compound and Mixed Poisson Representations
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 51 / Issue 1 / March 2014
- Published online by Cambridge University Press:
- 30 January 2018, pp. 19-36
- Print publication:
- March 2014
-
- Article
-
- You have access
- Export citation
A NEW FORMULA FOR ADOMIAN POLYNOMIALS AND THE ANALYSIS OF ITS TRUNCATED SERIES SOLUTION FOR FRACTIONAL NON-DIFFERENTIABLE INITIAL VALUE PROBLEMS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 55 / Issue 1 / July 2013
- Published online by Cambridge University Press:
- 20 November 2013, pp. 69-92
-
- Article
-
- You have access
- Export citation
METRIC DIFFERENTIABILITY OF LIPSCHITZ MAPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 96 / Issue 1 / February 2014
- Published online by Cambridge University Press:
- 15 October 2013, pp. 25-35
-
- Article
-
- You have access
- Export citation
ON A QUESTION OF J. M. RASSIAS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 89 / Issue 3 / June 2014
- Published online by Cambridge University Press:
- 27 September 2013, pp. 494-499
- Print publication:
- June 2014
-
- Article
-
- You have access
- Export citation
TOWARDS DIFFERENTIAL CALCULUS IN STRATIFIED GROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 95 / Issue 1 / August 2013
- Published online by Cambridge University Press:
- 17 June 2013, pp. 76-128
-
- Article
-
- You have access
- Export citation
SYSTEMS OF ISLANDS WITH CONTINUOUS HEIGHT FUNCTIONS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 94 / Issue 3 / June 2013
- Published online by Cambridge University Press:
- 01 May 2013, pp. 385-396
-
- Article
-
- You have access
- Export citation
Bounds and algorithms for the
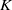 $K$ -Bessel function of imaginary order
$K$ -Bessel function of imaginary order
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 16 / October 2013
- Published online by Cambridge University Press:
- 10 April 2013, pp. 78-108
-
- Article
-
- You have access
- Export citation
COMPLETE MONOTONICITY OF A FUNCTION INVOLVING THE DIVIDED DIFFERENCE OF PSI FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 88 / Issue 2 / October 2013
- Published online by Cambridge University Press:
- 18 January 2013, pp. 309-319
- Print publication:
- October 2013
-
- Article
-
- You have access
- Export citation
GENERALISATIONS OF INTEGRAL INEQUALITIES OF HERMITE–HADAMARD TYPE THROUGH CONVEXITY
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 88 / Issue 2 / October 2013
- Published online by Cambridge University Press:
- 20 December 2012, pp. 320-330
- Print publication:
- October 2013
-
- Article
-
- You have access
- Export citation
A SOBOLEV ALGEBRA OF VOLTERRA TYPE
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 92 / Issue 3 / June 2012
- Published online by Cambridge University Press:
- 12 December 2012, pp. 313-334
-
- Article
-
- You have access
- Export citation
ON THE RANKIN–SELBERG ZETA FUNCTION
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 93 / Issue 1-2 / October 2012
- Published online by Cambridge University Press:
- 19 September 2012, pp. 101-113
-
- Article
-
- You have access
- Export citation
ON THE POSITIVITY OF RIEMANN–STIELTJES INTEGRALS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 87 / Issue 3 / June 2013
- Published online by Cambridge University Press:
- 02 August 2012, pp. 400-405
- Print publication:
- June 2013
-
- Article
-
- You have access
- Export citation
ON CONTINUOUS SOLUTIONS OF AN EQUATION OF THE GOŁA̧B–SCHINZEL TYPE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 87 / Issue 1 / February 2013
- Published online by Cambridge University Press:
- 15 May 2012, pp. 10-17
- Print publication:
- February 2013
-
- Article
-
- You have access
- Export citation
NEIGHBORLINESS OF THE SYMMETRIC MOMENT CURVE
- Part of
-
- Journal:
- Mathematika / Volume 59 / Issue 1 / January 2013
- Published online by Cambridge University Press:
- 12 April 2012, pp. 223-249
- Print publication:
- January 2013
-
- Article
- Export citation
ON SOME REFINEMENTS AND CONVERSES OF MULTIDIMENSIONAL HILBERT-TYPE INEQUALITIES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 85 / Issue 3 / June 2012
- Published online by Cambridge University Press:
- 06 March 2012, pp. 380-394
- Print publication:
- June 2012
-
- Article
-
- You have access
- Export citation
A Fourier Approach for the Level Crossings of Shot Noise Processes with Jumps
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 49 / Issue 1 / March 2012
- Published online by Cambridge University Press:
- 04 February 2016, pp. 100-113
- Print publication:
- March 2012
-
- Article
-
- You have access
- Export citation
ON PERIODIC SOLUTIONS FOR FIRST-ORDER DIFFERENTIAL EQUATIONS INVOLVING THE DISTRIBUTIONAL HENSTOCK–KURZWEIL INTEGRAL
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 86 / Issue 2 / October 2012
- Published online by Cambridge University Press:
- 06 February 2012, pp. 327-338
- Print publication:
- October 2012
-
- Article
-
- You have access
- Export citation
A GENERALISATION OF DESCARTES’ RULE OF SIGNS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 91 / Issue 3 / December 2011
- Published online by Cambridge University Press:
- 24 January 2012, pp. 415-420
-
- Article
-
- You have access
- Export citation