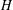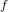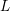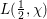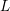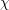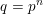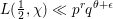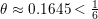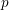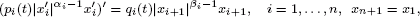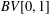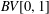Refine listing
Actions for selected content:
325 results in 26xxx
FRACTIONAL MODELS IN SPACE FOR DIFFUSIVE PROCESSES IN HETEROGENEOUS MEDIA WITH APPLICATIONS IN CELL MOTILITY AND ELECTRICAL SIGNAL PROPAGATION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 93 / Issue 3 / June 2016
- Published online by Cambridge University Press:
- 10 February 2016, pp. 518-520
- Print publication:
- June 2016
-
- Article
-
- You have access
- Open access
- Export citation
Exact Solutions for Fractional Differential-Difference Equations by (G'/G)-Expansion Method with Modified Riemann-Liouville Derivative
- Part of
-
- Journal:
- Advances in Applied Mathematics and Mechanics / Volume 8 / Issue 2 / April 2016
- Published online by Cambridge University Press:
- 27 January 2016, pp. 293-305
- Print publication:
- April 2016
-
- Article
- Export citation
BUZANO’S INEQUALITY HOLDS FOR ANY PROJECTION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 93 / Issue 3 / June 2016
- Published online by Cambridge University Press:
- 20 January 2016, pp. 504-510
- Print publication:
- June 2016
-
- Article
-
- You have access
- Export citation
A parallel root-finding algorithm
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 18 / Issue 1 / 2015
- Published online by Cambridge University Press:
- 01 December 2015, pp. 713-729
-
- Article
-
- You have access
- Export citation
Sub-Weyl subconvexity for Dirichlet
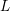 $L$-functions to prime power moduli
$L$-functions to prime power moduli
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 4 / April 2016
- Published online by Cambridge University Press:
- 03 November 2015, pp. 825-875
- Print publication:
- April 2016
-
- Article
- Export citation
Convolution estimates for singular measures and some global nonlinear Brascamp—Lieb inequalities
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 145 / Issue 6 / December 2015
- Published online by Cambridge University Press:
- 08 October 2015, pp. 1223-1237
- Print publication:
- December 2015
-
- Article
- Export citation
On strongly decreasing solutions of cyclic systems of second-order nonlinear differential equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 145 / Issue 5 / October 2015
- Published online by Cambridge University Press:
- 02 September 2015, pp. 1007-1028
- Print publication:
- October 2015
-
- Article
- Export citation
UNIFORMLY BOUNDED COMPOSITION OPERATORS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 92 / Issue 3 / December 2015
- Published online by Cambridge University Press:
- 30 July 2015, pp. 463-469
- Print publication:
- December 2015
-
- Article
-
- You have access
- Export citation
LOCAL BOUNDEDNESS OF NONAUTONOMOUS SUPERPOSITION OPERATORS IN
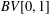 $BV[0,1]$
$BV[0,1]$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 92 / Issue 2 / October 2015
- Published online by Cambridge University Press:
- 08 July 2015, pp. 325-341
- Print publication:
- October 2015
-
- Article
-
- You have access
- Export citation
Diagonals of Separately Absolutely Continuous Mappings Coincide with the Sums of Absolutely Convergent Series of Continuous Functions
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 59 / Issue 2 / May 2016
- Published online by Cambridge University Press:
- 10 June 2015, pp. 435-444
-
- Article
- Export citation
EXACT UPPER AND LOWER BOUNDS ON THE DIFFERENCE BETWEEN THE ARITHMETIC AND GEOMETRIC MEANS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 92 / Issue 1 / August 2015
- Published online by Cambridge University Press:
- 04 May 2015, pp. 149-158
- Print publication:
- August 2015
-
- Article
-
- You have access
- Export citation
REFINING RECURSIVELY THE HERMITE–HADAMARD INEQUALITY ON A SIMPLEX
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 92 / Issue 1 / August 2015
- Published online by Cambridge University Press:
- 17 April 2015, pp. 57-67
- Print publication:
- August 2015
-
- Article
-
- You have access
- Export citation
MULTIFRACTAL ANALYSIS OF FUNCTIONS ON HEISENBERG AND CARNOT GROUPS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 16 / Issue 1 / February 2017
- Published online by Cambridge University Press:
- 27 March 2015, pp. 1-38
- Print publication:
- February 2017
-
- Article
- Export citation
State-Dependent Fractional Point Processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 52 / Issue 1 / March 2015
- Published online by Cambridge University Press:
- 30 January 2018, pp. 18-36
- Print publication:
- March 2015
-
- Article
-
- You have access
- Export citation
CONCAVITY PROPERTIES OF EXTENSIONS OF THE PARALLEL VOLUME
- Part of
-
- Journal:
- Mathematika / Volume 62 / Issue 1 / 2016
- Published online by Cambridge University Press:
- 13 January 2015, pp. 266-282
- Print publication:
- 2016
-
- Article
- Export citation
SOME COMMENTS ON SCALAR DIFFERENTIATION OF VECTOR-VALUED FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 91 / Issue 2 / April 2015
- Published online by Cambridge University Press:
- 11 November 2014, pp. 311-321
- Print publication:
- April 2015
-
- Article
-
- You have access
- Export citation
FRACTIONAL SOBOLEV–POINCARÉ AND FRACTIONAL HARDY INEQUALITIES IN UNBOUNDED JOHN DOMAINS
- Part of
-
- Journal:
- Mathematika / Volume 61 / Issue 2 / May 2015
- Published online by Cambridge University Press:
- 20 October 2014, pp. 385-401
- Print publication:
- May 2015
-
- Article
- Export citation
SHARP CONSTANTS IN THE POINCARÉ, STEKLOV AND RELATED INEQUALITIES (A SURVEY)
- Part of
-
- Journal:
- Mathematika / Volume 61 / Issue 2 / May 2015
- Published online by Cambridge University Press:
- 10 October 2014, pp. 328-344
- Print publication:
- May 2015
-
- Article
- Export citation
THE REFLEXIVITY INDEX OF A LATTICE OF SETS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 97 / Issue 2 / October 2014
- Published online by Cambridge University Press:
- 25 July 2014, pp. 237-250
- Print publication:
- October 2014
-
- Article
-
- You have access
- Export citation
BORNOLOGIES AND LOCALLY LIPSCHITZ FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 90 / Issue 2 / October 2014
- Published online by Cambridge University Press:
- 15 May 2014, pp. 257-263
- Print publication:
- October 2014
-
- Article
-
- You have access
- Export citation