Refine listing
Actions for selected content:
325 results in 26xxx
A New Family of Difference Schemes for Space Fractional Advection Diffusion Equation
- Part of
-
- Journal:
- Advances in Applied Mathematics and Mechanics / Volume 9 / Issue 2 / April 2017
- Published online by Cambridge University Press:
- 09 January 2017, pp. 282-306
- Print publication:
- April 2017
-
- Article
- Export citation
On the Global Gaussian Lipschitz Space
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 60 / Issue 3 / August 2017
- Published online by Cambridge University Press:
- 03 January 2017, pp. 707-720
-
- Article
- Export citation
ISOMETRIC REPRESENTATION OF LIPSCHITZ-FREE SPACES OVER CONVEX DOMAINS IN FINITE-DIMENSIONAL SPACES
- Part of
-
- Journal:
- Mathematika / Volume 63 / Issue 2 / 2017
- Published online by Cambridge University Press:
- 04 April 2017, pp. 538-552
- Print publication:
- 2017
-
- Article
- Export citation
BRASCAMP–LIEB INEQUALITY AND QUANTITATIVE VERSIONS OF HELLY’S THEOREM
- Part of
-
- Journal:
- Mathematika / Volume 63 / Issue 1 / 2017
- Published online by Cambridge University Press:
- 07 December 2016, pp. 272-291
- Print publication:
- 2017
-
- Article
- Export citation
COMPACT SPACES OF THE FIRST BAIRE CLASS THAT HAVE OPEN FINITE DEGREE
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 17 / Issue 5 / November 2018
- Published online by Cambridge University Press:
- 21 November 2016, pp. 1173-1196
- Print publication:
- November 2018
-
- Article
- Export citation
SHARP INEQUALITIES FOR THE VARIATION OF THE DISCRETE MAXIMAL FUNCTION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 95 / Issue 1 / February 2017
- Published online by Cambridge University Press:
- 04 November 2016, pp. 94-107
- Print publication:
- February 2017
-
- Article
-
- You have access
- Export citation
Numerical Solution of Euler-Lagrange Equation with Caputo Derivatives
- Part of
-
- Journal:
- Advances in Applied Mathematics and Mechanics / Volume 9 / Issue 1 / February 2017
- Published online by Cambridge University Press:
- 11 October 2016, pp. 173-185
- Print publication:
- February 2017
-
- Article
- Export citation
ON THE VARIATIONAL CONSTANT ASSOCIATED TO THE
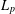 $L_{p}$ -HARDY INEQUALITY
$L_{p}$ -HARDY INEQUALITY
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 102 / Issue 3 / June 2017
- Published online by Cambridge University Press:
- 23 September 2016, pp. 405-419
-
- Article
-
- You have access
- Export citation
Multivariate fractional Poisson processes and compound sums
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 48 / Issue 3 / September 2016
- Published online by Cambridge University Press:
- 19 September 2016, pp. 691-711
- Print publication:
- September 2016
-
- Article
- Export citation
Jacobi Spectral Collocation Method for the Time Variable-Order Fractional Mobile-Immobile Advection-Dispersion Solute Transport Model
- Part of
-
- Journal:
- East Asian Journal on Applied Mathematics / Volume 6 / Issue 3 / August 2016
- Published online by Cambridge University Press:
- 20 July 2016, pp. 337-352
- Print publication:
- August 2016
-
- Article
- Export citation
Stable laws and Beurling kernels
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 48 / Issue A / July 2016
- Published online by Cambridge University Press:
- 25 July 2016, pp. 239-248
- Print publication:
- July 2016
-
- Article
- Export citation
THE COST–TIME CURVE FOR AN OPTIMAL TRAIN JOURNEY ON LEVEL TRACK
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 58 / Issue 1 / July 2016
- Published online by Cambridge University Press:
- 01 July 2016, pp. 10-32
-
- Article
-
- You have access
- Export citation
Fischer Decomposition and Cauchy–Kovalevskaya Extension in Fractional Clifford Analysis: The Riemann–Liouville Case
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 60 / Issue 1 / February 2017
- Published online by Cambridge University Press:
- 13 June 2016, pp. 251-272
-
- Article
- Export citation
A NEW EXAMPLE OF A DETERMINISTIC CHAOS GAME
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 94 / Issue 3 / December 2016
- Published online by Cambridge University Press:
- 02 June 2016, pp. 464-470
- Print publication:
- December 2016
-
- Article
-
- You have access
- Export citation
Mappings of Lp-integrable distortion: regularity of the inverse
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 146 / Issue 3 / June 2016
- Published online by Cambridge University Press:
- 16 May 2016, pp. 647-663
- Print publication:
- June 2016
-
- Article
- Export citation
Optimal rearrangement invariant range for Hardy-type operators
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 146 / Issue 4 / August 2016
- Published online by Cambridge University Press:
- 12 May 2016, pp. 865-893
- Print publication:
- August 2016
-
- Article
- Export citation
Bruckner–Garg-Type Results with Respect to Haar Null Sets in C[0, 1]
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 60 / Issue 1 / February 2017
- Published online by Cambridge University Press:
- 10 May 2016, pp. 17-30
-
- Article
- Export citation
Multilevel Circulant Preconditioner for High-Dimensional Fractional Diffusion Equations
- Part of
-
- Journal:
- East Asian Journal on Applied Mathematics / Volume 6 / Issue 2 / May 2016
- Published online by Cambridge University Press:
- 12 May 2016, pp. 109-130
- Print publication:
- May 2016
-
- Article
- Export citation
On a partial theta function and its spectrum
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 146 / Issue 3 / June 2016
- Published online by Cambridge University Press:
- 19 April 2016, pp. 609-623
- Print publication:
- June 2016
-
- Article
- Export citation
A Second-Order Finite Difference Method for Two-Dimensional Fractional Percolation Equations
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 19 / Issue 3 / March 2016
- Published online by Cambridge University Press:
- 16 March 2016, pp. 733-757
- Print publication:
- March 2016
-
- Article
- Export citation
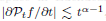 , where
, where 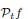 is the Poisson integral of the function
is the Poisson integral of the function 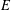
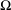
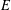
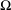
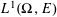
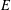
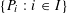
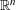
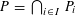
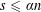
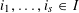
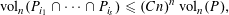
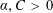


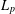
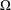
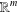
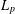
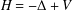
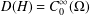
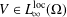
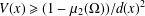
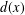

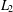
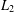
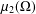


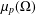
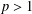
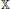 be an open set in ℝ
be an open set in ℝ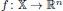 is a Sobolev homeomorphism. We study the regularity of
is a Sobolev homeomorphism. We study the regularity of 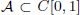 is
is 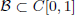 and a Borel probability measure
and a Borel probability measure 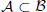 and
and 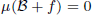 for all
for all 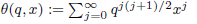 defines a
defines a 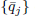 of values of
of values of 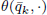 has a double real zero
has a double real zero 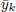 (the rest of its real zeros being simple). For
(the rest of its real zeros being simple). For 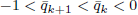 . One has
. One has 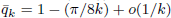 and
and 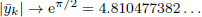 .
.