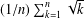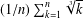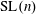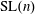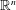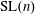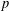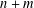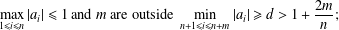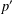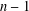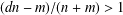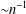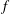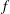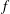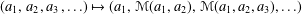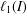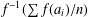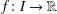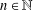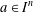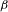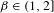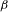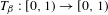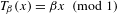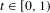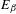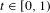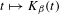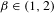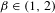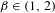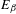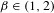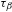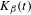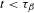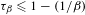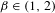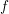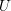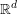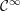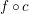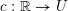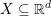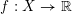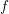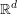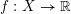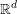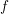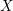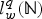Refine listing
Actions for selected content:
325 results in 26xxx
INEQUALITIES FOR DRAGOMIR’S MAPPINGS VIA STIELTJES INTEGRALS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 102 / Issue 2 / October 2020
- Published online by Cambridge University Press:
- 16 January 2020, pp. 240-250
- Print publication:
- October 2020
-
- Article
-
- You have access
- Export citation
INEQUALITIES OF JENSEN’S TYPE FOR POSITIVE LINEAR FUNCTIONALS ON HERMITIAN UNITAL BANACH
 $\ast$-ALGEBRAS
$\ast$-ALGEBRAS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 102 / Issue 2 / October 2020
- Published online by Cambridge University Press:
- 08 January 2020, pp. 308-318
- Print publication:
- October 2020
-
- Article
-
- You have access
- Export citation
ALGEBRAIC STRUCTURE OF THE RANGE OF A TRIGONOMETRIC POLYNOMIAL
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 102 / Issue 2 / October 2020
- Published online by Cambridge University Press:
- 08 January 2020, pp. 251-260
- Print publication:
- October 2020
-
- Article
-
- You have access
- Export citation
ODD–EVEN DECOMPOSITION OF FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 102 / Issue 1 / August 2020
- Published online by Cambridge University Press:
- 08 January 2020, pp. 104-108
- Print publication:
- August 2020
-
- Article
-
- You have access
- Export citation
THE FLOOR OF THE ARITHMETIC MEAN OF THE CUBE ROOTS OF THE FIRST
 $n$ INTEGERS
$n$ INTEGERS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 102 / Issue 2 / October 2020
- Published online by Cambridge University Press:
- 08 January 2020, pp. 261-267
- Print publication:
- October 2020
-
- Article
-
- You have access
- Export citation
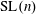 $\text{SL}(n)$ Invariant Valuations on Super-Coercive Convex Functions
$\text{SL}(n)$ Invariant Valuations on Super-Coercive Convex Functions
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 73 / Issue 1 / February 2021
- Published online by Cambridge University Press:
- 25 October 2019, pp. 108-130
- Print publication:
- February 2021
-
- Article
- Export citation
NUMERICAL INVESTIGATION AND APPLICATION OF FRACTIONAL DYNAMICAL SYSTEMS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 101 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 23 October 2019, pp. 163-165
- Print publication:
- February 2020
-
- Article
-
- You have access
- Export citation
FKN theorem for the multislice, with applications
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 29 / Issue 2 / March 2020
- Published online by Cambridge University Press:
- 18 October 2019, pp. 200-212
-
- Article
- Export citation
A STABILITY VERSION OF THE GAUSS–LUCAS THEOREM AND APPLICATIONS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 109 / Issue 2 / October 2020
- Published online by Cambridge University Press:
- 05 September 2019, pp. 262-269
-
- Article
-
- You have access
- Export citation
Persistence probability of a random polynomial arising from evolutionary game theory
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 56 / Issue 3 / September 2019
- Published online by Cambridge University Press:
- 01 October 2019, pp. 870-890
- Print publication:
- September 2019
-
- Article
- Export citation
New sharp Hardy and Rellich type inequalities on Cartan–Hadamard manifolds and their improvements
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 6 / December 2020
- Published online by Cambridge University Press:
- 23 August 2019, pp. 2952-2981
- Print publication:
- December 2020
-
- Article
- Export citation
A new proof of the Hardy–Rellich inequality in any dimension
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 6 / December 2020
- Published online by Cambridge University Press:
- 19 August 2019, pp. 2894-2904
- Print publication:
- December 2020
-
- Article
- Export citation
Orlicz Addition for Measures and an Optimization Problem for the
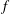 $f$-divergence
$f$-divergence
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 72 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 16 July 2019, pp. 455-479
- Print publication:
- April 2020
-
- Article
-
- You have access
- Export citation
WEAKENING OF THE HARDY PROPERTY FOR MEANS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 101 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 09 July 2019, pp. 118-129
- Print publication:
- February 2020
-
- Article
-
- You have access
- Export citation
A comparison principle for convolution measures with applications
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 169 / Issue 2 / September 2020
- Published online by Cambridge University Press:
- 28 June 2019, pp. 307-322
- Print publication:
- September 2020
-
- Article
- Export citation
Quasiconvex relaxation of isotropic functions in incompressible planar hyperelasticity
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 5 / October 2020
- Published online by Cambridge University Press:
- 11 June 2019, pp. 2620-2631
- Print publication:
- October 2020
-
- Article
-
- You have access
- Open access
- Export citation
CHARACTERIZATIONS OF QUASICONVEX AND PSEUDOCONVEX FUNCTIONS BY THEIR SECOND-ORDER REGULAR SUBDIFFERENTIALS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 109 / Issue 2 / October 2020
- Published online by Cambridge University Press:
- 30 April 2019, pp. 217-229
-
- Article
-
- You have access
- Export citation
The
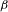 $\unicode[STIX]{x1D6FD}$-transformation with a hole at 0
$\unicode[STIX]{x1D6FD}$-transformation with a hole at 0
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 9 / September 2020
- Published online by Cambridge University Press:
- 25 March 2019, pp. 2482-2514
- Print publication:
- September 2020
-
- Article
-
- You have access
- Open access
- Export citation
Arc-smooth functions on closed sets
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 4 / April 2019
- Published online by Cambridge University Press:
- 15 March 2019, pp. 645-680
- Print publication:
- April 2019
-
- Article
- Export citation
Higher Summability and Discrete Weighted Muckenhoupt and Gehring Type Inequalities
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 62 / Issue 4 / November 2019
- Published online by Cambridge University Press:
- 11 March 2019, pp. 949-973
-
- Article
- Export citation