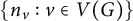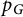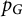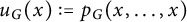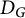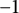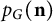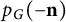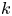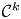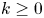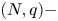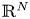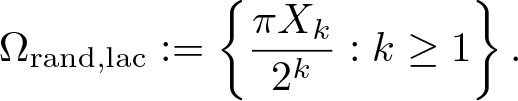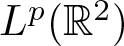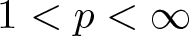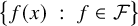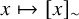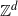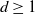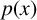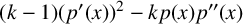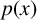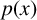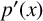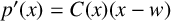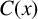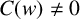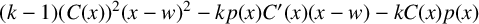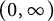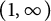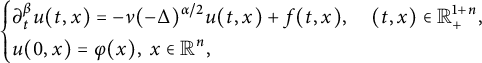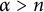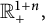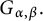Refine listing
Actions for selected content:
325 results in 26xxx
The blowup-polynomial of a metric space: connections to stable polynomials, graphs and their distance spectra
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 6 / December 2024
- Published online by Cambridge University Press:
- 09 November 2023, pp. 2073-2114
- Print publication:
- December 2024
-
- Article
- Export citation
Approximation and homotopy in regulous geometry
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 09 November 2023, pp. 1-20
- Print publication:
- January 2024
-
- Article
- Export citation
Topological regularity of isoperimetric sets in PI spaces having a deformation property
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 155 / Issue 2 / April 2025
- Published online by Cambridge University Press:
- 09 October 2023, pp. 611-633
- Print publication:
- April 2025
-
- Article
- Export citation
A weighted Trudinger–Moser inequalities and applications to some weighted $(N,q)-$
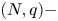 Laplacian equation in $\mathbb {R}^N$
Laplacian equation in $\mathbb {R}^N$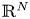 with new exponential growth conditions
with new exponential growth conditions
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 155 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 07 September 2023, pp. 124-175
- Print publication:
- February 2025
-
- Article
- Export citation
Perron’s capacity of random sets
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 66 / Issue 4 / November 2023
- Published online by Cambridge University Press:
- 01 September 2023, pp. 960-970
-
- Article
- Export citation
ON SEPARATE CONTINUITY AND SEPARATE CONVEXITY: A SYNTHETIC TREATMENT FOR FUNCTIONS AND SETS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 3 / June 2024
- Published online by Cambridge University Press:
- 17 July 2023, pp. 541-551
- Print publication:
- June 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Uncertainty principles in holomorphic function spaces on the unit ball
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 10 July 2023, pp. 122-136
- Print publication:
- March 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Sparse analytic systems
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 04 July 2023, e58
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Differences between Lyapunov exponents for the simple random walk in Bernoulli potentials
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 23 June 2023, pp. 82-103
- Print publication:
- March 2024
-
- Article
- Export citation
Multifractal analysis of sums of random pulses
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 175 / Issue 3 / November 2023
- Published online by Cambridge University Press:
- 22 June 2023, pp. 569-593
- Print publication:
- November 2023
-
- Article
- Export citation
Is the Sacker–Sell type spectrum equal to the contractible set?
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 03 March 2023, pp. 353-380
- Print publication:
- April 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON THE NUMBER OF REAL ZEROS OF POLYNOMIALS OF EVEN DEGREE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 27 February 2023, pp. 89-93
- Print publication:
- February 2024
-
- Article
- Export citation
Multisummability for generalized power series
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 27 February 2023, pp. 458-494
- Print publication:
- April 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Shape sensitivity of the Hardy constant involving the distance from a boundary submanifold
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 22 February 2023, pp. 408-423
- Print publication:
- April 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Extending linear growth functionals to functions of bounded fractional variation
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 21 February 2023, pp. 304-327
- Print publication:
- February 2024
-
- Article
- Export citation
REVERSED HARDY–LITTLEWOOD–PÓLYA INEQUALITIES WITH FINITE TERMS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 3 / December 2023
- Published online by Cambridge University Press:
- 03 February 2023, pp. 459-463
- Print publication:
- December 2023
-
- Article
- Export citation
CONSTRUCTING NONSTANDARD HULLS AND LOEB MEASURES IN INTERNAL SET THEORIES
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 29 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 14 December 2022, pp. 97-127
- Print publication:
- March 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Application of capacities to space–time fractional dissipative equations I: regularity and the blow-up set
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 6 / December 2023
- Published online by Cambridge University Press:
- 25 October 2022, pp. 1904-1956
- Print publication:
- December 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The Halász–Székely barycenter
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 65 / Issue 4 / November 2022
- Published online by Cambridge University Press:
- 13 October 2022, pp. 881-911
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Some analytical properties of the matrix related to q-coloured Delannoy numbers
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 65 / Issue 3 / August 2022
- Published online by Cambridge University Press:
- 06 October 2022, pp. 847-860
-
- Article
- Export citation