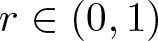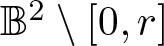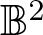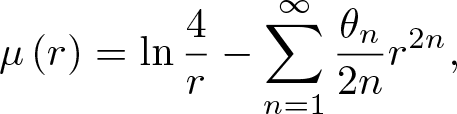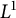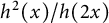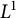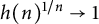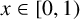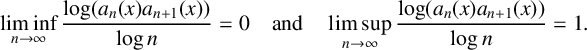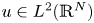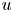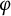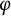Refine listing
Actions for selected content:
325 results in 26xxx
Series expansion, higher-order monotonicity properties and inequalities for the modulus of the Grötzsch ring
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 68 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 15 November 2024, pp. 16-43
-
- Article
- Export citation
A note on the space of all Toeplitz operators
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 12 November 2024, pp. 1123-1140
- Print publication:
- December 2024
-
- Article
- Export citation
A unified characterization of convolution coefficients in nonlocal differential equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 18 September 2024, pp. 1-19
-
- Article
- Export citation
Optimal transport through a toll station
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 36 / Issue 3 / June 2025
- Published online by Cambridge University Press:
- 18 September 2024, pp. 613-637
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On some convexity questions of Handelman
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 16 May 2024, pp. 936-939
- Print publication:
- December 2024
-
- Article
- Export citation
On the smoothness of slowly varying functions
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 3 / August 2024
- Published online by Cambridge University Press:
- 16 May 2024, pp. 876-891
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ASYMPTOTIC BEHAVIOUR FOR PRODUCTS OF CONSECUTIVE PARTIAL QUOTIENTS IN CONTINUED FRACTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 110 / Issue 3 / December 2024
- Published online by Cambridge University Press:
- 18 April 2024, pp. 448-459
- Print publication:
- December 2024
-
- Article
- Export citation
Sharp conditions for the validity of the Bourgain–Brezis–Mironescu formula
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 16 April 2024, pp. 1-24
-
- Article
- Export citation
Uniqueness and Hyers–Ulam’s stability for a fractional nonlinear partial integro-differential equation with variable coefficients and a mixed boundary condition
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 77 / Issue 4 / August 2025
- Published online by Cambridge University Press:
- 16 April 2024, pp. 1377-1397
- Print publication:
- August 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
An alternative approach to solenoidal Lipschitz truncation
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 155 / Issue 6 / December 2025
- Published online by Cambridge University Press:
- 05 April 2024, pp. 2296-2320
- Print publication:
- December 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Sobolev trace-type inequalities via time-space fractional heat equations
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 77 / Issue 4 / August 2025
- Published online by Cambridge University Press:
- 25 March 2024, pp. 1093-1134
- Print publication:
- August 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Theoretical study of a
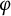 $\varphi $-Hilfer fractional differential system in Banach spaces
$\varphi $-Hilfer fractional differential system in Banach spaces
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 27 February 2024, pp. 742-759
- Print publication:
- September 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A UNIFIED APPROACH TO HINDMAN, RAMSEY, AND VAN DER WAERDEN SPACES
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 12 February 2024, pp. 1-53
-
- Article
- Export citation
Karamata’s theorem for regularized Cauchy transforms
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 155 / Issue 4 / August 2025
- Published online by Cambridge University Press:
- 26 January 2024, pp. 1431-1491
- Print publication:
- August 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Multidimensional Frank–Laptev–Weidl improvement of the hardy inequality
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 11 January 2024, pp. 151-167
-
- Article
- Export citation
Absolute concentration robustness and multistationarity in reaction networks: Conditions for coexistence
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 35 / Issue 4 / August 2024
- Published online by Cambridge University Press:
- 02 January 2024, pp. 566-600
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Slices of the Takagi function
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 9 / September 2024
- Published online by Cambridge University Press:
- 20 December 2023, pp. 2361-2398
- Print publication:
- September 2024
-
- Article
- Export citation
Nonlinear Beltrami equation: lower estimates of Schwarz lemma’s type
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 29 November 2023, pp. 533-543
- Print publication:
- September 2024
-
- Article
- Export citation
Selection principles and proofs from the Book
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 23 November 2023, pp. 478-492
- Print publication:
- June 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
t-Design Curves and Mobile Sampling on the Sphere
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 23 November 2023, e105
-
- Article
-
- You have access
- Open access
- HTML
- Export citation