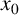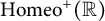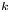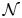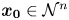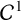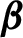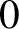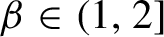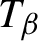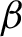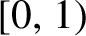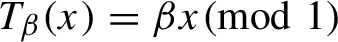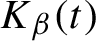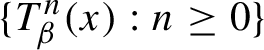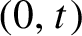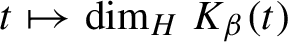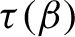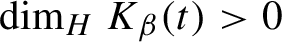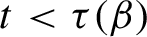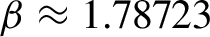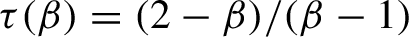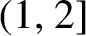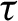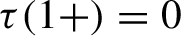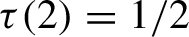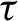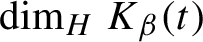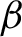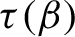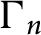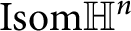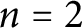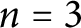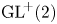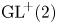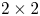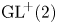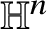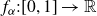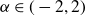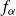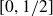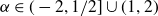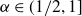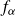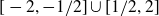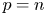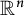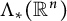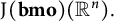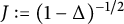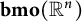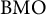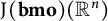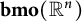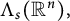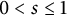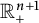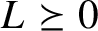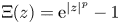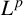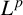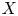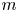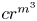Refine listing
Actions for selected content:
325 results in 26xxx
QUASICONTINUITY, NONATTRACTING POINTS, DISTRIBUTIVE CHAOS AND RESISTANCE TO DISRUPTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 107 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 06 October 2022, pp. 102-111
- Print publication:
- February 2023
-
- Article
- Export citation
On a class of Hilbert-type inequalities in the whole plane involving some classical kernel functions
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 65 / Issue 3 / August 2022
- Published online by Cambridge University Press:
- 06 October 2022, pp. 833-846
-
- Article
- Export citation
How robustly can you predict the future?
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 5 / October 2023
- Published online by Cambridge University Press:
- 07 September 2022, pp. 1493-1515
- Print publication:
- October 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the analyticity of WLUD∞ functions of one variable and WLUD∞ functions of several variables in a complete non-Archimedean valued field
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 65 / Issue 3 / August 2022
- Published online by Cambridge University Press:
- 07 July 2022, pp. 691-704
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
106.29 An improvement on the Garfunkel-Bankoff inequality
- Part of
-
- Journal:
- The Mathematical Gazette / Volume 106 / Issue 566 / July 2022
- Published online by Cambridge University Press:
- 22 June 2022, pp. 342-344
- Print publication:
- July 2022
-
- Article
- Export citation
REGULARITY OF AML FUNCTIONS IN TWO-DIMENSIONAL NORMED SPACES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 114 / Issue 3 / June 2023
- Published online by Cambridge University Press:
- 20 May 2022, pp. 406-430
- Print publication:
- June 2023
-
- Article
- Export citation
Critical values for the
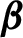 $\boldsymbol{\beta} $-transformation with a hole at
$\boldsymbol{\beta} $-transformation with a hole at 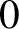 $0$
$0$
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 6 / June 2023
- Published online by Cambridge University Press:
- 02 May 2022, pp. 1785-1828
- Print publication:
- June 2023
-
- Article
- Export citation
Hyperbolic Coxeter groups of minimal growth rates in higher dimensions
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 06 April 2022, pp. 232-242
- Print publication:
- March 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A rank-one convex, nonpolyconvex isotropic function on
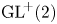 $\textrm {GL}^{\!+}(2)$ with compact connected sublevel sets
$\textrm {GL}^{\!+}(2)$ with compact connected sublevel sets
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 152 / Issue 2 / April 2022
- Published online by Cambridge University Press:
- 02 February 2022, pp. 356-381
- Print publication:
- April 2022
-
- Article
- Export citation
Lipschitz graphs and currents in Heisenberg groups
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 02 February 2022, e6
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Step roots of Littlewood polynomials and the extrema of functions in the Takagi class
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 173 / Issue 3 / November 2022
- Published online by Cambridge University Press:
- 24 January 2022, pp. 591-618
- Print publication:
- November 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Series expansion of Leray–Trudinger inequality
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 20 December 2021, pp. 262-274
- Print publication:
- February 2023
-
- Article
- Export citation
On a backward problem for nonlinear time fractional wave equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 152 / Issue 6 / December 2022
- Published online by Cambridge University Press:
- 24 November 2021, pp. 1589-1612
- Print publication:
- December 2022
-
- Article
- Export citation
Approximation in the Zygmund and Hölder classes on
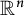 $\mathbb {R}^n$
$\mathbb {R}^n$
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 74 / Issue 6 / December 2022
- Published online by Cambridge University Press:
- 13 September 2021, pp. 1745-1770
- Print publication:
- December 2022
-
- Article
- Export citation
Hilbert’s 17th problem in free skew fields
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 06 September 2021, e61
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the initial value problem for a class of nonlinear biharmonic equation with time-fractional derivative
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 152 / Issue 4 / August 2022
- Published online by Cambridge University Press:
- 26 August 2021, pp. 989-1031
- Print publication:
- August 2022
-
- Article
- Export citation
Lorentz and Gale–Ryser theorems on general measure spaces
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 152 / Issue 4 / August 2022
- Published online by Cambridge University Press:
- 09 August 2021, pp. 857-878
- Print publication:
- August 2022
-
- Article
- Export citation
SOME
 $\boldsymbol {L^p}$-HARDY AND
$\boldsymbol {L^p}$-HARDY AND  $\boldsymbol {L^p}$-RELLICH TYPE INEQUALITIES WITH REMAINDER TERMS
$\boldsymbol {L^p}$-RELLICH TYPE INEQUALITIES WITH REMAINDER TERMS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 113 / Issue 1 / August 2022
- Published online by Cambridge University Press:
- 22 June 2021, pp. 79-98
- Print publication:
- August 2022
-
- Article
- Export citation
EMBEDDING THEOREM OF THE WEIGHTED SOBOLEV–LORENTZ SPACES
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 64 / Issue 2 / May 2022
- Published online by Cambridge University Press:
- 10 June 2021, pp. 358-375
- Print publication:
- May 2022
-
- Article
- Export citation
Smooth parameterizations of power-subanalytic sets and compositions of Gevrey functions
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 64 / Issue 3 / August 2021
- Published online by Cambridge University Press:
- 04 June 2021, pp. 532-554
-
- Article
- Export citation