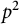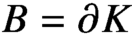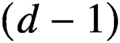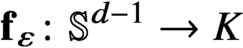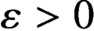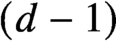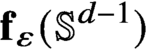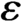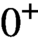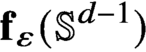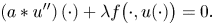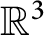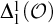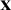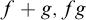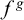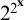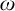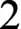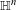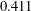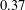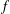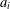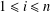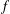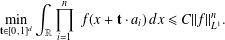Refine listing
Actions for selected content:
325 results in 26xxx
Log-concavity and log-convexity of moments of averages of i.i.d. random variables
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 03 May 2021, pp. 271-278
- Print publication:
- June 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Counting matchings via capacity-preserving operators
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 30 / Issue 6 / November 2021
- Published online by Cambridge University Press:
- 30 April 2021, pp. 956-981
-
- Article
-
- You have access
- Open access
- Export citation
On finite sections of the multiplicative Hilbert inequalities
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 1 / March 2022
- Published online by Cambridge University Press:
- 08 April 2021, pp. 208-216
- Print publication:
- March 2022
-
- Article
- Export citation
Continuous Maps from Spheres Converging to Boundaries of Convex Hulls
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 18 February 2021, e13
-
- Article
-
- You have access
- Open access
- Export citation
Sharp Caffarelli–Kohn–Nirenberg inequalities on Riemannian manifolds: the influence of curvature
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 152 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 22 January 2021, pp. 102-127
- Print publication:
- February 2022
-
- Article
- Export citation
STRICTLY REAL FUNDAMENTAL THEOREM OF ALGEBRA USING POLYNOMIAL INTERLACING
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 104 / Issue 2 / October 2021
- Published online by Cambridge University Press:
- 18 January 2021, pp. 249-255
- Print publication:
- October 2021
-
- Article
-
- You have access
- Open access
- Export citation
Existence and monotonicity of nonlocal boundary value problems: the one-dimensional case
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 152 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 23 December 2020, pp. 1-27
- Print publication:
- February 2022
-
- Article
- Export citation
A characterization of singular Schrödinger operators on the half-line
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 07 December 2020, pp. 923-941
- Print publication:
- December 2021
-
- Article
- Export citation
A dichotomy of sets via typical differentiability
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 8 / 2020
- Published online by Cambridge University Press:
- 04 November 2020, e41
-
- Article
-
- You have access
- Open access
- Export citation
LUZIN’S (N) AND RANDOMNESS REFLECTION
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 87 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 30 October 2020, pp. 802-828
- Print publication:
- June 2022
-
- Article
- Export citation
ASYMPTOTIC ANALYSIS OF SKOLEM’S EXPONENTIAL FUNCTIONS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 87 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 04 September 2020, pp. 758-782
- Print publication:
- June 2022
-
- Article
- Export citation
Lineability, continuity, and antiderivatives in the non-Archimedean setting
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 02 September 2020, pp. 638-650
- Print publication:
- September 2021
-
- Article
- Export citation
DECOMPOSING FUNCTIONS OF BAIRE CLASS
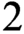 $2$ ON POLISH SPACES
$2$ ON POLISH SPACES
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 85 / Issue 3 / September 2020
- Published online by Cambridge University Press:
- 26 October 2020, pp. 960-971
- Print publication:
- September 2020
-
- Article
- Export citation
BASES FOR FUNCTIONS BEYOND THE FIRST BAIRE CLASS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 85 / Issue 3 / September 2020
- Published online by Cambridge University Press:
- 27 October 2020, pp. 1289-1303
- Print publication:
- September 2020
-
- Article
- Export citation
Mixing and average mixing times for general Markov processes
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 14 August 2020, pp. 541-552
- Print publication:
- September 2021
-
- Article
-
- You have access
- Open access
- Export citation
Hardy type inequalities on closed manifolds via Ricci curvature
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 3 / June 2021
- Published online by Cambridge University Press:
- 21 July 2020, pp. 993-1020
- Print publication:
- June 2021
-
- Article
- Export citation
POINCARÉ AND SOBOLEV INEQUALITIES FOR DIFFERENTIAL FORMS IN HEISENBERG GROUPS AND CONTACT MANIFOLDS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 3 / May 2022
- Published online by Cambridge University Press:
- 29 June 2020, pp. 869-920
- Print publication:
- May 2022
-
- Article
-
- You have access
- Open access
- Export citation
AN ALTERNATIVE APPROACH TO FRÉCHET DERIVATIVES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 111 / Issue 2 / October 2021
- Published online by Cambridge University Press:
- 14 May 2020, pp. 202-220
- Print publication:
- October 2021
-
- Article
- Export citation
EXTENSIONS OF AUTOCORRELATION INEQUALITIES WITH APPLICATIONS TO ADDITIVE COMBINATORICS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 102 / Issue 3 / December 2020
- Published online by Cambridge University Press:
- 08 April 2020, pp. 451-461
- Print publication:
- December 2020
-
- Article
-
- You have access
- Export citation
Embeddings of homogeneous Sobolev spaces on the entire space
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 1 / February 2021
- Published online by Cambridge University Press:
- 09 March 2020, pp. 296-328
- Print publication:
- February 2021
-
- Article
- Export citation