Refine listing
Actions for selected content:
321 results in 26xxx
FRACTIONAL INTEGRAL OPERATORS IN NONHOMOGENEOUS SPACES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 80 / Issue 2 / October 2009
- Published online by Cambridge University Press:
- 29 June 2009, pp. 324-334
- Print publication:
- October 2009
-
- Article
-
- You have access
- Export citation
ON WEIGHTED INEQUALITIES WITH GEOMETRIC MEAN OPERATOR
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 78 / Issue 3 / December 2008
- Published online by Cambridge University Press:
- 01 December 2008, pp. 463-475
- Print publication:
- December 2008
-
- Article
-
- You have access
- Export citation
Some Blackwell-Type Renewal Theorems for Weighted Renewal Functions
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 45 / Issue 4 / December 2008
- Published online by Cambridge University Press:
- 14 July 2016, pp. 972-993
- Print publication:
- December 2008
-
- Article
-
- You have access
- Export citation
ON A GLOBAL UPPER BOUND FOR JESSEN’S INEQUALITY
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 50 / Issue 2 / October 2008
- Published online by Cambridge University Press:
- 01 October 2008, pp. 246-257
-
- Article
-
- You have access
- Export citation
BOUNDS FOR THE DEVIATION OF A FUNCTION FROM THE CHORD GENERATED BY ITS EXTREMITIES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 78 / Issue 2 / October 2008
- Published online by Cambridge University Press:
- 01 October 2008, pp. 225-248
- Print publication:
- October 2008
-
- Article
-
- You have access
- Export citation
NEW GRONWALL–OU-IANG TYPE INTEGRAL INEQUALITIES AND THEIR APPLICATIONS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 50 / Issue 1 / July 2008
- Published online by Cambridge University Press:
- 01 July 2008, pp. 111-127
-
- Article
-
- You have access
- Export citation
THE FUNDAMENTAL AND NUMERICAL SOLUTIONS OF THE RIESZ SPACE-FRACTIONAL REACTION–DISPERSION EQUATION
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 50 / Issue 1 / July 2008
- Published online by Cambridge University Press:
- 01 July 2008, pp. 45-57
-
- Article
-
- You have access
- Export citation
ANOTHER SHARP L2 INEQUALITY OF OSTROWSKI TYPE
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 50 / Issue 1 / July 2008
- Published online by Cambridge University Press:
- 01 July 2008, pp. 129-136
-
- Article
-
- You have access
- Export citation
ARITHMETIC MEAN OF VALUES AND VALUE AT MEAN OF ARGUMENTS FOR CONVEX FUNCTIONS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 50 / Issue 1 / July 2008
- Published online by Cambridge University Press:
- 01 July 2008, pp. 137-141
-
- Article
-
- You have access
- Export citation
INEQUALITIES FOR SUPERADDITIVE FUNCTIONALS WITH APPLICATIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 77 / Issue 3 / June 2008
- Published online by Cambridge University Press:
- 01 June 2008, pp. 401-411
- Print publication:
- June 2008
-
- Article
-
- You have access
- Export citation
A NEW MEAN WITH INEQUALITIES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 77 / Issue 3 / June 2008
- Published online by Cambridge University Press:
- 01 June 2008, pp. 365-371
- Print publication:
- June 2008
-
- Article
-
- You have access
- Export citation
MULTIDIMENSIONAL HARDY-TYPE INEQUALITIES VIA CONVEXITY
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 77 / Issue 2 / April 2008
- Published online by Cambridge University Press:
- 01 April 2008, pp. 245-260
- Print publication:
- April 2008
-
- Article
-
- You have access
- Export citation
APPROXIMATING THE STIELTJES INTEGRAL FOR (φ,Φ)-LIPSCHITZIAN INTEGRATORS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 77 / Issue 1 / February 2008
- Published online by Cambridge University Press:
- 01 February 2008, pp. 73-90
- Print publication:
- February 2008
-
- Article
-
- You have access
- Export citation
A SHARP L2 INEQUALITY OF OSTROWSKI TYPE
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 49 / Issue 3 / January 2008
- Published online by Cambridge University Press:
- 01 January 2008, pp. 423-429
-
- Article
-
- You have access
- Export citation
General convex stochastic orderings and related martingale-type structures
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 39 / Issue 1 / March 2007
- Published online by Cambridge University Press:
- 01 July 2016, pp. 105-127
- Print publication:
- March 2007
-
- Article
-
- You have access
- Export citation
Multivariate subexponential distributions and random sums of random vectors
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 38 / Issue 4 / December 2006
- Published online by Cambridge University Press:
- 08 September 2016, pp. 1028-1046
- Print publication:
- December 2006
-
- Article
-
- You have access
- Export citation
Some completely monotonic functions involving the gamma and polygamma functions
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 80 / Issue 1 / February 2006
- Published online by Cambridge University Press:
- 09 April 2009, pp. 81-88
- Print publication:
- February 2006
-
- Article
-
- You have access
- Export citation
Volterra spaces revisited
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 79 / Issue 1 / August 2005
- Published online by Cambridge University Press:
- 09 April 2009, pp. 61-76
- Print publication:
- August 2005
-
- Article
-
- You have access
- Export citation
Limit theorem for continuous-time random walks with two time scales
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 41 / Issue 2 / June 2004
- Published online by Cambridge University Press:
- 14 July 2016, pp. 455-466
- Print publication:
- June 2004
-
- Article
- Export citation
Box–Cox transformations and heavy-tailed distributions
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 41 / Issue A / 2004
- Published online by Cambridge University Press:
- 14 July 2016, pp. 213-227
- Print publication:
- 2004
-
- Article
- Export citation
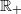 for some positive constants
for some positive constants 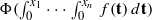 instead of
instead of 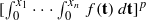 , while the corresponding right-hand sides remain as in the classical Hardy’s inequality and have explicit constants in front of integrals. We also prove the related dual inequalities. The relations obtained are new even for the one-dimensional case and they unify and extend several inequalities of Hardy type known in the literature.
, while the corresponding right-hand sides remain as in the classical Hardy’s inequality and have explicit constants in front of integrals. We also prove the related dual inequalities. The relations obtained are new even for the one-dimensional case and they unify and extend several inequalities of Hardy type known in the literature.