Refine listing
Actions for selected content:
321 results in 26xxx
Some inequalities that arise in measure theory
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 45 / Issue 1 / August 1988
- Published online by Cambridge University Press:
- 09 April 2009, pp. 83-94
- Print publication:
- August 1988
-
- Article
-
- You have access
- Export citation
An Inequality Implicit Function Theorem
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 44 / Issue 2 / April 1988
- Published online by Cambridge University Press:
- 09 April 2009, pp. 146-150
- Print publication:
- April 1988
-
- Article
-
- You have access
- Export citation
An extension theorem for convex functions and an application to Teicher's characterization of the normal distribution
- Part of
-
- Journal:
- Mathematika / Volume 34 / Issue 2 / December 1987
- Published online by Cambridge University Press:
- 26 February 2010, pp. 155-159
- Print publication:
- December 1987
-
- Article
- Export citation
The multidimensional fundamental theorem of calculus
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 43 / Issue 2 / October 1987
- Published online by Cambridge University Press:
- 09 April 2009, pp. 143-170
- Print publication:
- October 1987
-
- Article
-
- You have access
- Export citation
On the convexity and symmetry of solutions to an elliptic free boundary problem
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 42 / Issue 1 / February 1987
- Published online by Cambridge University Press:
- 09 April 2009, pp. 57-68
- Print publication:
- February 1987
-
- Article
-
- You have access
- Export citation
A function is Perron integrable if it has locally small Riemann sums
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 41 / Issue 2 / October 1986
- Published online by Cambridge University Press:
- 09 April 2009, pp. 224-232
- Print publication:
- October 1986
-
- Article
-
- You have access
- Export citation
A Riemann integral in a locally compact Hausdorff space
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 41 / Issue 1 / August 1986
- Published online by Cambridge University Press:
- 09 April 2009, pp. 115-137
- Print publication:
- August 1986
-
- Article
-
- You have access
- Export citation
Some inequalities for trigonometric polynomials
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 39 / Issue 2 / October 1985
- Published online by Cambridge University Press:
- 09 April 2009, pp. 216-226
- Print publication:
- October 1985
-
- Article
-
- You have access
- Export citation
Time-dependent Lipschitz attractors for non-semigroup evolution processes
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 38 / Issue 1 / February 1985
- Published online by Cambridge University Press:
- 09 April 2009, pp. 103-117
- Print publication:
- February 1985
-
- Article
-
- You have access
- Export citation
Denjoy-Bochner almost periodic functions
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 37 / Issue 2 / October 1984
- Published online by Cambridge University Press:
- 09 April 2009, pp. 205-222
- Print publication:
- October 1984
-
- Article
-
- You have access
- Export citation
(PVB) functions and integration
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 36 / Issue 3 / June 1984
- Published online by Cambridge University Press:
- 09 April 2009, pp. 335-353
- Print publication:
- June 1984
-
- Article
-
- You have access
- Export citation
A problem in two-dimensional integration
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 35 / Issue 3 / December 1983
- Published online by Cambridge University Press:
- 09 April 2009, pp. 386-404
- Print publication:
- December 1983
-
- Article
-
- You have access
- Export citation
The Burkill approximately continuous integral
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 35 / Issue 2 / October 1983
- Published online by Cambridge University Press:
- 09 April 2009, pp. 236-253
- Print publication:
- October 1983
-
- Article
-
- You have access
- Export citation
A note on the index laws of fractional calculus
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 34 / Issue 3 / June 1983
- Published online by Cambridge University Press:
- 09 April 2009, pp. 356-363
- Print publication:
- June 1983
-
- Article
-
- You have access
- Export citation
An analytic inequality
- Part of
-
- Journal:
- Mathematika / Volume 30 / Issue 1 / June 1983
- Published online by Cambridge University Press:
- 26 February 2010, pp. 142-152
- Print publication:
- June 1983
-
- Article
- Export citation
Integration by parts for the generalized Riemann-Stieltjes integral
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 34 / Issue 2 / April 1983
- Published online by Cambridge University Press:
- 09 April 2009, pp. 229-233
- Print publication:
- April 1983
-
- Article
-
- You have access
- Export citation
Some Inequalities arising from a Banach algebra norm
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 34 / Issue 2 / April 1983
- Published online by Cambridge University Press:
- 09 April 2009, pp. 199-202
- Print publication:
- April 1983
-
- Article
-
- You have access
- Export citation
Components of an open set
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 33 / Issue 2 / October 1982
- Published online by Cambridge University Press:
- 09 April 2009, pp. 249-261
- Print publication:
- October 1982
-
- Article
-
- You have access
- Export citation
The existence of locally fine simplicial subdivisions
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 33 / Issue 1 / August 1982
- Published online by Cambridge University Press:
- 09 April 2009, pp. 114-124
- Print publication:
- August 1982
-
- Article
-
- You have access
- Export citation
Convergence in kth variation and RSk integrals
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 31 / Issue 2 / August 1981
- Published online by Cambridge University Press:
- 09 April 2009, pp. 163-174
- Print publication:
- August 1981
-
- Article
-
- You have access
- Export citation
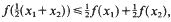
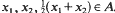 .
. 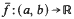
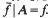 .
.