Refine listing
Actions for selected content:
325 results in 26xxx
Still more generalizations of Hardy's inequality
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 59 / Issue 2 / October 1995
- Published online by Cambridge University Press:
- 09 April 2009, pp. 214-224
-
- Article
-
- You have access
- Export citation
The Burkill approximately continuous integral
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 35 / Issue 2 / October 1983
- Published online by Cambridge University Press:
- 09 April 2009, pp. 236-253
-
- Article
-
- You have access
- Export citation
A note on the index laws of fractional calculus
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 34 / Issue 3 / June 1983
- Published online by Cambridge University Press:
- 09 April 2009, pp. 356-363
-
- Article
-
- You have access
- Export citation
Franel integrals of order four
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 60 / Issue 2 / April 1996
- Published online by Cambridge University Press:
- 09 April 2009, pp. 192-203
-
- Article
-
- You have access
- Export citation
A problem in two-dimensional integration
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 35 / Issue 3 / December 1983
- Published online by Cambridge University Press:
- 09 April 2009, pp. 386-404
-
- Article
-
- You have access
- Export citation
Fourier series with small gaps
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 46 / Issue 2 / April 1989
- Published online by Cambridge University Press:
- 09 April 2009, pp. 212-219
-
- Article
-
- You have access
- Export citation
Components of an open set
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 33 / Issue 2 / October 1982
- Published online by Cambridge University Press:
- 09 April 2009, pp. 249-261
-
- Article
-
- You have access
- Export citation
A function is Perron integrable if it has locally small Riemann sums
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 41 / Issue 2 / October 1986
- Published online by Cambridge University Press:
- 09 April 2009, pp. 224-232
-
- Article
-
- You have access
- Export citation
(PVB) functions and integration
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 36 / Issue 3 / June 1984
- Published online by Cambridge University Press:
- 09 April 2009, pp. 335-353
-
- Article
-
- You have access
- Export citation
Denjoy-Bochner almost periodic functions
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 37 / Issue 2 / October 1984
- Published online by Cambridge University Press:
- 09 April 2009, pp. 205-222
-
- Article
-
- You have access
- Export citation
Continuity properties of the superposition operator
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 47 / Issue 2 / October 1989
- Published online by Cambridge University Press:
- 09 April 2009, pp. 186-210
-
- Article
-
- You have access
- Export citation
On Ψ direct sums of Banach spaces and convexity
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 75 / Issue 3 / December 2003
- Published online by Cambridge University Press:
- 09 April 2009, pp. 413-422
-
- Article
-
- You have access
- Export citation
Convergence in kth variation and RSk integrals
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 31 / Issue 2 / August 1981
- Published online by Cambridge University Press:
- 09 April 2009, pp. 163-174
-
- Article
-
- You have access
- Export citation
Some inequalities of Bessel and modified Bessel functions
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 50 / Issue 2 / April 1991
- Published online by Cambridge University Press:
- 09 April 2009, pp. 333-342
-
- Article
-
- You have access
- Export citation
On some reverse integral inequalities
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 49 / Issue 2 / October 1990
- Published online by Cambridge University Press:
- 09 April 2009, pp. 319-326
-
- Article
-
- You have access
- Export citation
Bounds for the separations of real zeros of polynomials
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 59 / Issue 3 / December 1995
- Published online by Cambridge University Press:
- 09 April 2009, pp. 330-342
-
- Article
-
- You have access
- Export citation
A Riemann integral in a locally compact Hausdorff space
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 41 / Issue 1 / August 1986
- Published online by Cambridge University Press:
- 09 April 2009, pp. 115-137
-
- Article
-
- You have access
- Export citation
The zeros of linear combinations of translates of polynomials
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 72 / Issue 1 / February 2002
- Published online by Cambridge University Press:
- 09 April 2009, pp. 109-118
-
- Article
-
- You have access
- Export citation
Sums of Cantor sets yielding an interval
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 73 / Issue 3 / December 2002
- Published online by Cambridge University Press:
- 09 April 2009, pp. 405-418
-
- Article
-
- You have access
- Export citation
Volterra spaces revisited
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 79 / Issue 1 / August 2005
- Published online by Cambridge University Press:
- 09 April 2009, pp. 61-76
-
- Article
-
- You have access
- Export citation
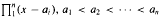 by δ(
by δ(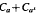 is an interval if and only if a /(1−2
is an interval if and only if a /(1−2