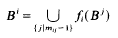Refine listing
Actions for selected content:
321 results in 26xxx
Two gradient properties of explicitly convex functions
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 58 / Issue 3 / June 1995
- Published online by Cambridge University Press:
- 09 April 2009, pp. 404-410
- Print publication:
- June 1995
-
- Article
-
- You have access
- Export citation
Markoff type inequalities for curved majorants
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 58 / Issue 1 / February 1995
- Published online by Cambridge University Press:
- 09 April 2009, pp. 1-14
- Print publication:
- February 1995
-
- Article
-
- You have access
- Export citation
Insertion of a measurable function
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 57 / Issue 3 / December 1994
- Published online by Cambridge University Press:
- 09 April 2009, pp. 295-304
- Print publication:
- December 1994
-
- Article
-
- You have access
- Export citation
A sharp inequality related to Moser's inequality
- Part of
-
- Journal:
- Mathematika / Volume 40 / Issue 2 / December 1993
- Published online by Cambridge University Press:
- 26 February 2010, pp. 357-366
- Print publication:
- December 1993
-
- Article
- Export citation
Limit theorems for convex hulls of random sets
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 25 / Issue 2 / June 1993
- Published online by Cambridge University Press:
- 01 July 2016, pp. 395-414
- Print publication:
- June 1993
-
- Article
- Export citation
Opial-type inequalities with m functions in n variables
- Part of
-
- Journal:
- Mathematika / Volume 39 / Issue 2 / December 1992
- Published online by Cambridge University Press:
- 26 February 2010, pp. 319-326
- Print publication:
- December 1992
-
- Article
- Export citation
Limit distributions for compounded sums of extreme order statistics
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 29 / Issue 3 / September 1992
- Published online by Cambridge University Press:
- 14 July 2016, pp. 557-574
- Print publication:
- September 1992
-
- Article
- Export citation
Certain inequalities involving fractional powers
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 53 / Issue 1 / August 1992
- Published online by Cambridge University Press:
- 09 April 2009, pp. 131-136
- Print publication:
- August 1992
-
- Article
-
- You have access
- Export citation
Concavity and reflected Lévy processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 29 / Issue 1 / March 1992
- Published online by Cambridge University Press:
- 14 July 2016, pp. 209-215
- Print publication:
- March 1992
-
- Article
- Export citation
Some inequalities of Bessel and modified Bessel functions
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 50 / Issue 2 / April 1991
- Published online by Cambridge University Press:
- 09 April 2009, pp. 333-342
- Print publication:
- April 1991
-
- Article
-
- You have access
- Export citation
On some reverse integral inequalities
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 49 / Issue 2 / October 1990
- Published online by Cambridge University Press:
- 09 April 2009, pp. 319-326
- Print publication:
- October 1990
-
- Article
-
- You have access
- Export citation
Sharp function estimates for fractional integrals and related operators
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 49 / Issue 1 / August 1990
- Published online by Cambridge University Press:
- 09 April 2009, pp. 129-137
- Print publication:
- August 1990
-
- Article
-
- You have access
- Export citation
Some new Opial-type inequalities
- Part of
-
- Journal:
- Mathematika / Volume 37 / Issue 1 / June 1990
- Published online by Cambridge University Press:
- 26 February 2010, pp. 136-142
- Print publication:
- June 1990
-
- Article
- Export citation
Integral inequalities resembling Copson's inequality
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 48 / Issue 1 / February 1990
- Published online by Cambridge University Press:
- 09 April 2009, pp. 124-132
- Print publication:
- February 1990
-
- Article
-
- You have access
- Export citation
Continuity properties of the superposition operator
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 47 / Issue 2 / October 1989
- Published online by Cambridge University Press:
- 09 April 2009, pp. 186-210
- Print publication:
- October 1989
-
- Article
-
- You have access
- Export citation
On Takagi Fractal Surfaces
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 32 / Issue 3 / 01 September 1989
- Published online by Cambridge University Press:
- 20 November 2018, pp. 377-384
- Print publication:
- 01 September 1989
-
- Article
-
- You have access
- Export citation
Ramsey type theorems for real functions
- Part of
-
- Journal:
- Mathematika / Volume 36 / Issue 1 / June 1989
- Published online by Cambridge University Press:
- 26 February 2010, pp. 131-141
- Print publication:
- June 1989
-
- Article
- Export citation
Fourier series with small gaps
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 46 / Issue 2 / April 1989
- Published online by Cambridge University Press:
- 09 April 2009, pp. 212-219
- Print publication:
- April 1989
-
- Article
-
- You have access
- Export citation
The maximum distribution of a Gaussian stochastic process indexed by a local field
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 46 / Issue 1 / February 1989
- Published online by Cambridge University Press:
- 09 April 2009, pp. 69-87
- Print publication:
- February 1989
-
- Article
-
- You have access
- Export citation
A generalization of mixed invariant sets
- Part of
-
- Journal:
- Mathematika / Volume 35 / Issue 2 / December 1988
- Published online by Cambridge University Press:
- 26 February 2010, pp. 198-206
- Print publication:
- December 1988
-
- Article
- Export citation
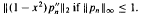
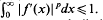 .
. , be i.i.d. random closed sets in
, be i.i.d. random closed sets in 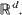 . Limit theorems for their normalized convex hulls
. Limit theorems for their normalized convex hulls 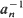 conv (
conv (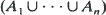 ) are proved. The limiting distributions correspond to
) are proved. The limiting distributions correspond to 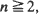 , the sets
, the sets 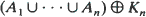 coincide in distribution for certain positive
coincide in distribution for certain positive