Refine listing
Actions for selected content:
34 results in 33Dxx
PARTIAL INDEFINITE THETA IDENTITIES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 102 / Issue 2 / April 2017
- Published online by Cambridge University Press:
- 19 September 2016, pp. 255-289
- Print publication:
- April 2017
-
- Article
-
- You have access
- Export citation
MOCK THETA DOUBLE SUMS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 59 / Issue 2 / May 2017
- Published online by Cambridge University Press:
- 10 June 2016, pp. 323-348
- Print publication:
- May 2017
-
- Article
-
- You have access
- Export citation
UNFOLDING THE DOUBLE SHUFFLE STRUCTURE OF
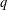 $q$-MULTIPLE ZETA VALUES
$q$-MULTIPLE ZETA VALUES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 91 / Issue 3 / June 2015
- Published online by Cambridge University Press:
- 24 April 2015, pp. 368-388
- Print publication:
- June 2015
-
- Article
-
- You have access
- Export citation
BGG reciprocity for current algebras
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 7 / July 2015
- Published online by Cambridge University Press:
- 09 February 2015, pp. 1265-1287
- Print publication:
- July 2015
-
- Article
- Export citation
FURTHER RESULTS ON VANISHING COEFFICIENTS IN INFINITE PRODUCT EXPANSIONS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 98 / Issue 1 / February 2015
- Published online by Cambridge University Press:
- 11 November 2014, pp. 69-77
- Print publication:
- February 2015
-
- Article
-
- You have access
- Export citation
MOCK THETA FUNCTIONS AND QUANTUM MODULAR FORMS
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 1 / 2013
- Published online by Cambridge University Press:
- 19 September 2013, e2
-
- Article
-
- You have access
- Open access
- Export citation
STATES ON THE CUNTZ ALGEBRAS AND p-ADIC RANDOM WALKS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 90 / Issue 2 / April 2011
- Published online by Cambridge University Press:
- 19 July 2011, pp. 197-211
- Print publication:
- April 2011
-
- Article
-
- You have access
- Export citation
Overpartitions and the q-Bailey identity
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 52 / Issue 2 / June 2009
- Published online by Cambridge University Press:
- 28 May 2009, pp. 297-306
-
- Article
-
- You have access
- Export citation
q-series and weight 3/2 Maass forms
- Part of
-
- Journal:
- Compositio Mathematica / Volume 145 / Issue 3 / May 2009
- Published online by Cambridge University Press:
- 01 May 2009, pp. 541-552
- Print publication:
- May 2009
-
- Article
-
- You have access
- Export citation
Mock Jacobi forms in basic hypergeometric series
- Part of
-
- Journal:
- Compositio Mathematica / Volume 145 / Issue 3 / May 2009
- Published online by Cambridge University Press:
- 01 May 2009, pp. 553-565
- Print publication:
- May 2009
-
- Article
-
- You have access
- Export citation
Bisymmetric functions, Macdonald polynomials and
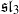 basic hypergeometric series
basic hypergeometric series
- Part of
-
- Journal:
- Compositio Mathematica / Volume 144 / Issue 2 / March 2008
- Published online by Cambridge University Press:
- 01 March 2008, pp. 271-303
- Print publication:
- March 2008
-
- Article
-
- You have access
- Export citation
Limit theorems for isotropic random walks on triangle buildings
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 73 / Issue 3 / December 2002
- Published online by Cambridge University Press:
- 09 April 2009, pp. 301-334
- Print publication:
- December 2002
-
- Article
-
- You have access
- Export citation
A new proof of the Macdonald identities for An−1
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 62 / Issue 3 / June 1997
- Published online by Cambridge University Press:
- 09 April 2009, pp. 345-360
- Print publication:
- June 1997
-
- Article
-
- You have access
- Export citation
Steady-state Markov chain models for the Heine and Euler distributions
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 29 / Issue 4 / December 1992
- Published online by Cambridge University Press:
- 14 July 2016, pp. 869-876
- Print publication:
- December 1992
-
- Article
- Export citation
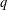
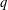
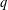
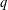
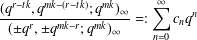
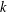
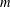


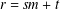
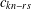
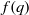
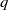
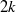
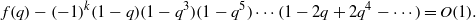
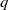
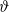
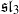 basic hypergeometric series
basic hypergeometric series
