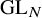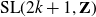Refine listing
Actions for selected content:
352 results in 22Exx
Geometric structures for maximal representations and pencils
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 14 / 2026
- Published online by Cambridge University Press:
- 16 February 2026, e23
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Positivity and representations of surface groups
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 14 / 2026
- Published online by Cambridge University Press:
- 09 February 2026, e6
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
LINEAR INDEPENDENCE OF QUANTUM TRANSLATES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 26 January 2026, pp. 1-7
-
- Article
- Export citation
ON RESIDUES OF INTERTWINING OPERATORS FOR HEISENBERG PARABOLIC SUBGROUPS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu , First View
- Published online by Cambridge University Press:
- 26 January 2026, pp. 1-214
-
- Article
- Export citation
Signature characters of invariant Hermitian forms on irreducible Verma modules of singular infinitesimal character and Hall–Littlewood polynomials
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 09 January 2026, pp. 1-23
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON EQUIVALENCE RELATIONS INDUCED BY POLISH GROUPS
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 29 December 2025, pp. 1-43
-
- Article
- Export citation
DETECTING IDEALS IN REDUCED CROSSED PRODUCT C*-ALGEBRAS OF TOPOLOGICAL DYNAMICAL SYSTEMS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu , First View
- Published online by Cambridge University Press:
- 16 December 2025, pp. 1-25
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Hyperbolic geometry and real moduli of five points on the line
- Part of
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Multiplicity one theorem for general Spin groups: The Archimedean case
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 28 November 2025, pp. 1-17
-
- Article
- Export citation
The dual pair
 $\mathrm {Aut}(C)\times F_{4}$ (p-adic case)
$\mathrm {Aut}(C)\times F_{4}$ (p-adic case)
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 16 October 2025, e174
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
DENOMINATORS IN LUSZTIG’S ASYMPTOTIC HECKE ALGEBRA VIA THE PLANCHEREL FORMULA
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 25 / Issue 1 / January 2026
- Published online by Cambridge University Press:
- 08 October 2025, pp. 285-337
- Print publication:
- January 2026
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
CHARACTERISATION OF DISTAL ACTIONS OF AUTOMORPHISMS ON THE SPACE OF ONE-PARAMETER SUBGROUPS OF LIE GROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 119 / Issue 2 / October 2025
- Published online by Cambridge University Press:
- 15 August 2025, pp. 152-175
-
- Article
- Export citation
EISENSTEIN COHOMOLOGY FOR ORTHOGONAL GROUPS AND THE SPECIAL VALUES OF L-FUNCTIONS FOR
 $\mathrm {GL}_1 \times \mathrm {O}(2n)$
$\mathrm {GL}_1 \times \mathrm {O}(2n)$
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 6 / November 2025
- Published online by Cambridge University Press:
- 28 July 2025, pp. 2463-2522
- Print publication:
- November 2025
-
- Article
- Export citation
Quaternionic Satake equivalence
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 7 / July 2025
- Published online by Cambridge University Press:
- 08 September 2025, pp. 1615-1663
- Print publication:
- July 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Tilting sheaves for real groups and Koszul duality
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 7 / July 2025
- Published online by Cambridge University Press:
- 11 September 2025, pp. 1698-1777
- Print publication:
- July 2025
-
- Article
- Export citation
Moments, Exponential Sums, and Monodromy Groups
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 26 June 2025, e101
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Eisenstein Cohomology for
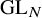 $\mathrm {GL}_N$ and the special values of Rankin–Selberg L-functions over a totally imaginary number field
$\mathrm {GL}_N$ and the special values of Rankin–Selberg L-functions over a totally imaginary number field
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 22 May 2025, e86
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Integral Zariski dense surface groups in
 $\textrm{SL}(n,\mathbf{R})$
$\textrm{SL}(n,\mathbf{R})$
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 179 / Issue 1 / July 2025
- Published online by Cambridge University Press:
- 13 May 2025, pp. 63-78
- Print publication:
- July 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The global Gan-Gross-Prasad conjecture for unitary groups. II. From Eisenstein series to Bessel periods
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 13 / 2025
- Published online by Cambridge University Press:
- 13 May 2025, e16
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Newell–Littlewood numbers III: Eigencones and GIT-semigroups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 5 / May 2025
- Published online by Cambridge University Press:
- 27 August 2025, pp. 1054-1074
- Print publication:
- May 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
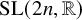
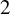
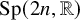














































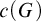
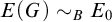
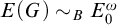
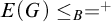
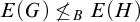
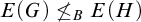
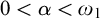
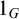
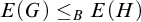
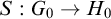
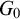
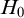
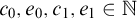
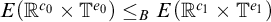
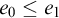
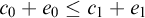






 -groupoid algebras to the general twisted setting.
-groupoid algebras to the general twisted setting.